class: middle, center <!--- https://katex.org/docs/supported.html#macros ---> $$ \global\def\myx#1{{\color{green}\mathbf{x}\_{#1}}} $$ $$ \global\def\myxa#1{{\color{green}\mathbf{x}\_{#1}^{(a)}}} $$ $$ \global\def\myza#1{{\color{green}\mathbf{z}\_{#1}^{(a)}}} $$ $$ \global\def\myxv#1{{\color{purple}\mathbf{x}\_{#1}^{(v)}}} $$ $$ \global\def\myzv#1{{\color{purple}\mathbf{z}\_{#1}^{(v)}}} $$ $$ \global\def\myzav#1{{\color{brown}\mathbf{z}\_{#1}^{(av)}}} $$ $$ \global\def\myzds#1{{\color{brown}\mathbf{z}\_{#1}^{(av)}}} $$ $$ \global\def\mywav{{\color{brown}\mathbf{w}^{(av)}}} $$ $$ \global\def\myw{{\color{brown}\mathbf{w}}} $$ $$ \global\def\mys#1{{\color{green}\mathbf{s}\_{#1}}} $$ $$ \global\def\myS#1{{\color{green}\mathbf{S}\_{#1}}} $$ $$ \global\def\myz#1{{\color{brown}\mathbf{z}\_{#1}}} $$ $$ \global\def\myztilde#1{{\color{brown}\tilde{\mathbf{z}}\_{#1}}} $$ $$ \global\def\myhnmf#1{{\color{brown}\mathbf{h}\_{#1}}} $$ $$ \global\def\myztilde#1{{\color{brown}\tilde{\mathbf{z}}\_{#1}}} $$ $$ \global\def\myu#1{\mathbf{u}\_{#1}} $$ $$ \global\def\mya#1{\mathbf{a}\_{#1}} $$ $$ \global\def\myv#1{\mathbf{v}\_{#1}} $$ $$ \global\def\mythetaz{\theta\_\myz{}} $$ $$ \global\def\mythetax{\theta\_\myx{}} $$ $$ \global\def\mythetas{\theta\_\mys{}} $$ $$ \global\def\mythetaa{\theta\_\mya{}} $$ $$ \global\def\bs#1{{\boldsymbol{#1}}} $$ $$ \global\def\diag{\text{diag}} $$ $$ \global\def\mbf{\mathbf} $$ $$ \global\def\myh#1{{\color{purple}\mbf{h}\_{#1}}} $$ $$ \global\def\myhfw#1{{\color{purple}\overrightarrow{\mbf{h}}\_{#1}}} $$ $$ \global\def\myhbw#1{{\color{purple}\overleftarrow{\mbf{h}}\_{#1}}} $$ $$ \global\def\myg#1{{\color{purple}\mbf{g}\_{#1}}} $$ $$ \global\def\mygfw#1{{\color{purple}\overrightarrow{\mbf{g}}\_{#1}}} $$ $$ \global\def\mygbw#1{{\color{purple}\overleftarrow{\mbf{g}}\_{#1}}} $$ $$ \global\def\neq{\mathrel{\char`≠}} $$ .vspace[ ] # A Multimodal Dynamical Variational Autoencoder for Audiovisual Speech Representation Learning .vspace[ ] .center.bold[Simon Leglaive] .small.center[CentraleSupélec, IETR (UMR CNRS 6164), France] .vspace[ ] .center.width-7[] .grid[ .kol-1-6[ .vspace[ ] .left.width-120[] ] .kol-2-3[ .small.center[Seminar @ LISTEN joint laboratory <br><br> Palaiseau (France) - January 12, 2023] ] .kol-1-6[ .vspace[ ] .right.width-65[]] ] --- class: middle ## Joint work with .grid[ .kol-1-4[ .center.width-90.circle-highlight[ <br/> **.bold[Samir Sadok]**<sup>.small[1]</sup>] ] .kol-1-4[ .center.width-90.circle[ <br/> Laurent Girin<sup>.small[2]</sup>] ] .kol-1-4[ .center.width-90.circle[ <br> Xavier Alameda-Pineda<sup>.small[3]</sup>] ] .kol-1-4[ .center.width-90.circle[ <br/> Renaud Séguier<sup>.small[1]</sup>] ] .kol-1-3[ .small.center[<sup>1</sup> CentraleSupélec, IETR (UMR CNRS 6164), France] ] .kol-1-3[ .small.center[<sup>2</sup> Univ. Grenoble Alpes, CNRS, Grenoble-INP, GIPSA-lab, France] ] .kol-1-3[ .small.center[<sup>3</sup> Inria, Univ. Grenoble Alpes, CNRS, LJK, France] ] ] --- class: middle .question.center[ .big[🚧] $\hspace{.5cm}$ .bold.big[Ongoing work] $\hspace{.5cm}$ .big[🚧] ] --- class: middle, center count: false # Introduction --- class: middle ## Supervised learning .center[The majority of successful applications of machine/deep learning rely on **supervised learning**.] .grid[ .kol-2-3[ .center[ <iframe width="600" height="310" src="https://www.youtube.com/embed/qWl9idsCuLQ?start=10&mute=1&loop=1&autoplay=1&playlist=qWl9idsCuLQ" frameborder="0" allow="autoplay; encrypted-media" style="max-width:100%" allowfullscreen=""></iframe> ] .center.small[Semantic urban image segmentation with ICNet (Zhao et al., 2018)] ] .kol-1-3[ .medium[ The Cityscapes dataset <br>.small[(Cordts et al., 2016)] - **5k images** with high quality pixel-level annotations - **1.5h** to annotate each single image .alert-90[More than 300 days of annotation! 😱] ] ] ] .alert[It is intractable to collect labels for every scenario and task.] <br> .credit[ M. Cordts et al., The Cityscapes dataset for semantic urban scene understanding, IEEE CVPR 2016 <br> Zhao et al., ICNet for real-time semantic segmentation on high-resolution images, ECCV 2018 ] --- ## Unsupervised learning .center[We need **unsupervised** methods that can learn to unveil the **underlying structure** of the data without or with few ground-truth labels.] .center.width-70[] .small.center[GENESIS (Engelcke et al., 2020), a generative model of 3D scenes capable of both decomposing and generating scenes by capturing relationships between scene components. Image credits: (Engelcke et al., 2020).] .alert[Deep latent variable generative models have emerged as promising approaches.] .credit[ M. Engelcke et al., GENESIS: Generative scene inference and sampling with object-centric latent representations, ICLR 2020. ] --- class: middle ## Generative modeling of structured high-dimensional data .center[**High-dimensional data** $\myx{} \in \mathbb{R}^d$ such as natural images or speech signals exhibit some form of **regularity**, preventing their dimensions from varying independently.] <br> .center.width-90[] .center[From a **generative perspective**, this regularity suggests that there exists a smaller dimensional **latent variable** $\myz{} \in \mathbb{R}^\ell$ that generated $\myx{} \in \mathbb{R}^d$, $\ell \ll d$.] .credit[Picture credits: <a href="https://fr.freepik.com/photos-gratuite/heureuse-fille-aux-cheveux-boucles-fait-signe-pouce-air-demontre-son-soutien-son-respect-quelqu-sourit-agreablement-atteint-objectif-souhaitable-porte-t-shirt-blanc-isole-mur-jaune_11932454.htm#query=black%20woman%20face&position=2&from_view=search">wayhomestudio</a> on Freepik. ] --- class: middle ## Latent-variable generative modeling .small-vspace[ ] .center.width-100[] <!-- $$ \hspace{1cm} \underbrace{p\_\theta(\myx{}) = \int p\_\theta(\myx{} |\myz{}) p(\myz{}) d\myz{}}\_{\text{model distribution}} \hspace{.25cm} \approx \hspace{-.5cm} \underbrace{\vphantom{\int}p^{\star}(\myx{})}\_{\text{true data distribution}} $$ --> - Generative modeling consists in estimating the parameters $\theta$ so that $p\_\theta(\myx{}) \approx p^\star(\myx{})$ according to some measure of fit, for instance the Kullback-Leibler (KL) divergence. - When the model includes a deep neural network, we obtain a **deep generative model**. --- class: middle ## The variational autoencoder (VAE) .tiny[(Kingma and Welling, 2014; Rezende et. al., 2014)] .grid[ .center.kol-3-5[ .center.kol-2-5[ .underline[Prior] $ \small p(\myz{}) = \mathcal{N}(\myz{}; \mathbf{0}, \mathbf{I})$ ] .center.kol-3-5[ .underline[Generative model] $ \small p\_\theta(\myx{} | \myz{}) = \mathcal{N}\left( \myx{}; \boldsymbol{\mu}\_\theta(\myz{}), \boldsymbol{\Sigma}\_\theta(\myz{}) \right) $ .small-vspace[ ] ] .center.width-90[] ] .center.kol-2-5[ .underline[Inference model] $\small q\_\phi(\myz{} | \myx{}) = \mathcal{N}\left( \myz{}; \boldsymbol{\mu}\_\phi(\myx{}), \boldsymbol{\Sigma}\_\phi(\myx{}) \right) \\\\$ <br> The inference model approximates the intractable exact posterior distribution $\displaystyle p\_\\theta(\myz{} | \myx{}) = \frac{p\_\theta(\myx{} | \myz{})p(\myz{})}{\int p\_\theta(\myx{} | \myz{})p(\myz{})d\myz{}}$ ] ] .small-nvspace[ ] $\footnotesize \hspace{.5cm} \boldsymbol{\Sigma}\_\phi(\myx{}) = \diag\\{ \mathbf{v}\_\phi(\myx{})\\} \qquad\qquad \boldsymbol{\Sigma}\_\theta(\myz{}) = \diag\\{ \mathbf{v}\_\theta(\myz{}) \\}$ .credit[ D.P. Kingma and M. Welling, Auto-encoding variational Bayes, ICLR 2014. <br> D.J. Rezende et al., Stochastic backpropagation and approximate inference in deep generative models, ICML 2014. ] --- class: middle The VAE parameters are estimated by maximizing the **evidence lower bound** (ELBO) .small[(Neal and Hinton, 1999; Jordan et al. 1999)] defined by: $$\begin{aligned} \mathcal{L}(\phi, \theta) &= \underbrace{\mathbb{E}\_{q\_\phi(\myz{} | \myx{})} [\ln p\_\theta(\myx{} | \myz{})]}\_{\text{reconstruction accuracy}} - \underbrace{D\_{\text{KL}}(q\_\phi(\myz{} | \myx{}) \parallel p(\myz{}))}\_{\text{regularization}}. \end{aligned} $$ The ELBO can also be decomposed as: $$\begin{aligned} \mathcal{L}(\phi, \theta) &= \ln p\_\theta(\myx{}) - D\_{\text{KL}}(q\_\phi(\myz{} | \myx{}) \parallel p\_\theta(\myz{} | \myx{})). \end{aligned} $$ .alert[ .left-column[ .underline[Generative model parameters estimation] $$ \underset{\theta}{\max}\, \Big\\{ \mathcal{L}(\phi, \theta) \le \ln p\_\theta(\myx{}) \Big\\} $$ ] .right-column[ .underline[Inference model parameters estimation] $$ \underset{\phi}{\max}\, \mathcal{L}(\phi, \theta) \,\,\Leftrightarrow\,\, \underset{\phi}{\min}\, D\_{\text{KL}}(q\_\phi(\myz{} | \myx{}) \parallel p\_\theta(\myz{} | \myx{}))$$ ] .reset-column[ ] ] .credit[ R.M. Neal and G.E. Hinton, A view of the EM algorithm that justifies incremental, sparse, and other variants, in M. I. Jordan (Ed.), .italic[Learning in graphical models], 1999. <br> M.I. Jordan et al., An introduction to variational methods for graphical models, Machine Learning, 1999.] --- - A trained VAE can be used for **generation**, **transformation**, and **downstream tasks**. - Ideally, the learned representation should be **disentangled** .small[(Higgins et al., 2018)], i.e., somehow easy to relate to independent and interpretable high-level characteristics of the data. .center.width-85[] .alert[Supervised learning from disentangled representations has been found to be more sample-efficient, more robust, and better in terms of generalization .small[(van Steenkiste et al., 2019)].] .credit[ .small-vspace[ ] I. Higgins et al., Towards a definition of disentangled representations. arXiv preprint arXiv:1812.02230, 2018. <br> S. Sadok et al., Learning and controlling the source-filter representation of speech with a variational autoencoder, arXiv preprint arXiv:2204.07075, 2022. <br> S. van Steenkiste et al., Are disentangled representations helpful for abstract visual reasoning?, NeurIPS, 2019. ] --- .small-nvspace[ ] .center[Over the past few years, the VAE has been extended in many ways, including for processing **dynamical** .bold[or] **multimodal** data.] <!-- .small[(Girin et al., 2021)] .small[(Suzuki et al., 2016; Wu and Goodman, 2018; Hsu and Glass, 2018; Shi et al., 2019, Sutter et al., 2021)] --> .center.width-90[] .alert[In this talk, we will present a multimodal .bold[and] dynamical VAE (MDVAE) applied to unsupervised audiovisual speech representation learning.] .credit[ .vspace[ ] L. Girin et al., Dynamical variational autoencoders: A comprehensive review, Foundations and Trends in Machine Learning, 2021. <br> M. Suzuki et al., Joint multimodal learning with deep denerative models, ICLR Workshop, 2017. <br> M. Wu and N. Goodman, Multimodal generative models for scalable weakly-supervised learning, NeurIPS, 2018. <br> W.-N. Hsu and J. R. Glass, Disentangling by partitioning: A representation learning framework for multimodal sensory data, arXiv preprint arXiv:1805.11264, 2018. <br> Y. Shi et al., Variational mixture-of-experts autoencoders for multi-modal deep denerative models, NeurIPS, 2019. <br> T. Sutter et al., Multimodal generative learning utilizing Jensen-Shannon divergence, NeurIPS, 2020. <br> T. Sutter et al., Generalized Multimodal ELBO, ICLR, 2021. ] --- ## Audiovisual (AV) speech latent factors .grid[ .kol-1-2[ .small-vspace[ ] .center[ <video controls width="500"> <source src="videos/W016_happy_level2_004.mp4" type="video/mp4"> </video> ] ] .kol-1-2[ - Speaker's identity and global emotional state <br> ↪ *static*, **shared** (AV) - Lip movements, phonemic information .small[(part of)] <br> ↪ *dynamical*, **shared** (AV) - Other facial movements and head pose <br> ↪ *dynamical*, **modality-specific** (V) - Pitch variations, phonemic information .small[(part of)] <br> ↪ *dynamical*, **modality-specific** (A) ] ] .alert[We seek to learn a multimodal dynamical VAE that disentangles these AV speech latent factors: dynamical and modality-specific, dynamical and audiovisual, static and audiovisual.] .credit[Video credits: K. Wang et al., MEAD: A large-scale audio-visual dataset for emotional talking-face generation, ECCV, 2020.] --- class: middle count: false .center[ # Multimodal dynamical VAE (MDVAE) ] <br> - .bold[Generative model] - Inference model - Two-stage training --- class: middle ## Notations .grid[ .kol-1-2[ .grid[ .kol-2-5[ $\myxa{} \in \mathbb{R}^{d\_a \times T}$ ] .kol-3-5[ **Observed** dynamical <font color="#258212">audio</font> data ] ] .small-nvspace[ ] .grid[ .kol-2-5[ $\myxv{} \in \mathbb{R}^{d\_v \times T}$ ] .kol-3-5[ **Observed** dynamical <font color="#800080">visual</font> data ] ] .small-vspace[ ] .grid[ .kol-2-5[ $\myw \in \mathbb{R}^{\ell\_w}$ ] .kol-3-5[ **Latent** static <font color="brown">audiovisual</font> data ] ] .small-nvspace[ ] .grid[ .kol-2-5[ $\myzav{} \in \mathbb{R}^{\ell\_{av} \times T}$ ] .kol-3-5[ **Latent** dynamical <font color="brown">audiovisual</font> data ] ] .small-nvspace[ ] .grid[ .kol-2-5[ $\myza{} \in \mathbb{R}^{\ell\_a \times T}$ ] .kol-3-5[ **Latent** dynamical <font color="#258212">audio</font> <br>data ] ] .small-nvspace[ ] .grid[ .kol-2-5[ $\myzv{} \in \mathbb{R}^{\ell\_v \times T}$ ] .kol-3-5[ **Latent** dynamical <font color="#800080">visual</font> data ] ] ] .kol-1-2[ .center.width-100[] ] ] --- class: middle ## MDVAE generative model - Defining the generative model amounts to defining the **joint distribution** of all variables: $$ p\_\theta\left(\myxa{}, \myxv{}, \myzav{},\myza{},\myzv{}, \myw{}\right). $$ By **structuring the dependencies** between these variables we hope to learn the desired disentangled representation of audiovisual speech in an **unsupervised** manner. - The temporal model in MDVAE is largely inspired by the **disentangled sequential autoencoder** (DSAE) of Li and Mandt (2018). MDVAE can be seen as a multimodal extension of DSAE. .credit[Y. Li and S. Mandt, "Disentangled sequential autoencoder", ICML 2018.] --- class: middle The global probabilistic graphical model of MDVAE is defined by the following Bayesian network. .center.width-100[] $$ \hspace{-.75cm} \small p\_\theta\left(\myxa{}, \myxv{}, \myzav{},\myza{},\myzv{}, \myw{}\right) = p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) p\_\theta\left(\myxv{} \mid \myzav{}, \myzv{}, \myw{}\right) p\_\theta\left(\myzav{}\right)p\_\theta\left(\myza{}\right) p\_\theta\left(\myzv{}\right)p\_\theta\left(\myw{}\right) $$ --- class: middle count: false The global probabilistic graphical model of MDVAE is defined by the following Bayesian network. .center.width-100[] $$ \hspace{-.75cm} \small p\_\theta\left(\myxa{}, \myxv{}, \myzav{},\myza{},\myzv{}, \myw{}\right) = \boxed{p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right)}p\_\theta\left(\myxv{} \mid \myzav{}, \myzv{}, \myw{}\right) p\_\theta\left(\myzav{}\right)p\_\theta\left(\myza{}\right) p\_\theta\left(\myzv{}\right)p\_\theta\left(\myw{}\right) $$ --- class: middle count: false The global probabilistic graphical model of MDVAE is defined by the following Bayesian network. .center.width-100[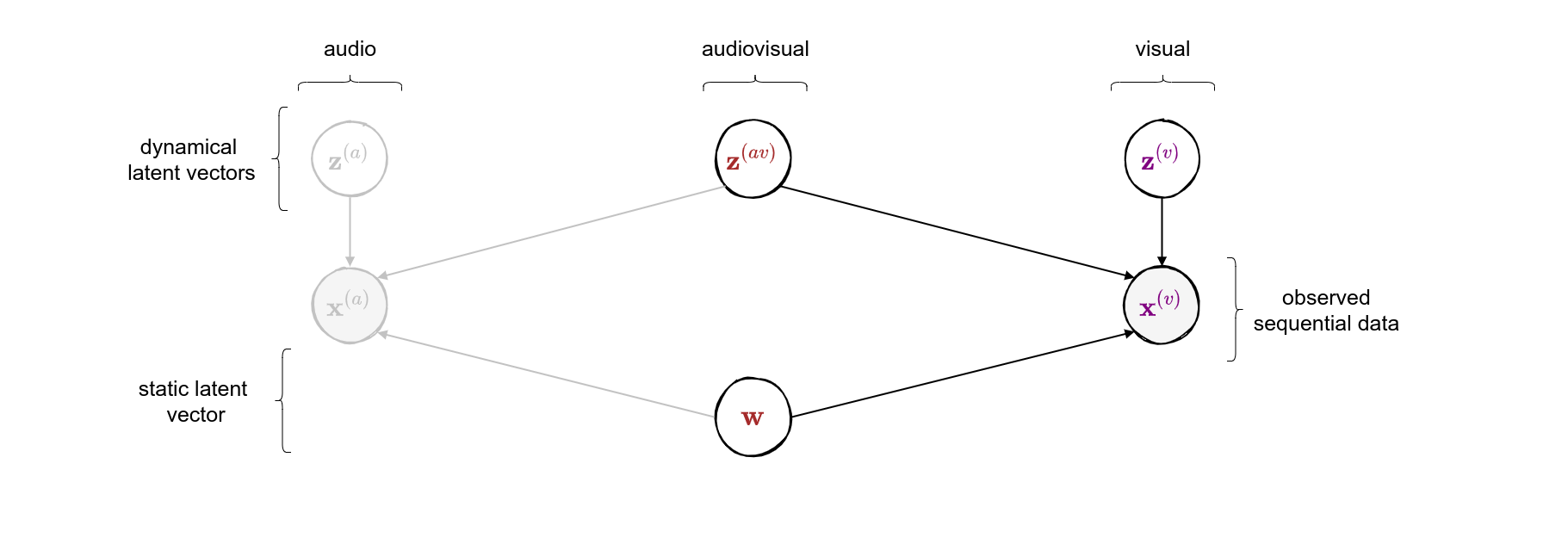] $$ \hspace{-.75cm} \small p\_\theta\left(\myxa{}, \myxv{}, \myzav{},\myza{},\myzv{}, \myw{}\right) = p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right)\boxed{p\_\theta\left(\myxv{} \mid \myzav{}, \myzv{}, \myw{}\right)} p\_\theta\left(\myzav{}\right)p\_\theta\left(\myza{}\right) p\_\theta\left(\myzv{}\right)p\_\theta\left(\myw{}\right) $$ --- class: middle count: false The global probabilistic graphical model of MDVAE is defined by the following Bayesian network. .center.width-100[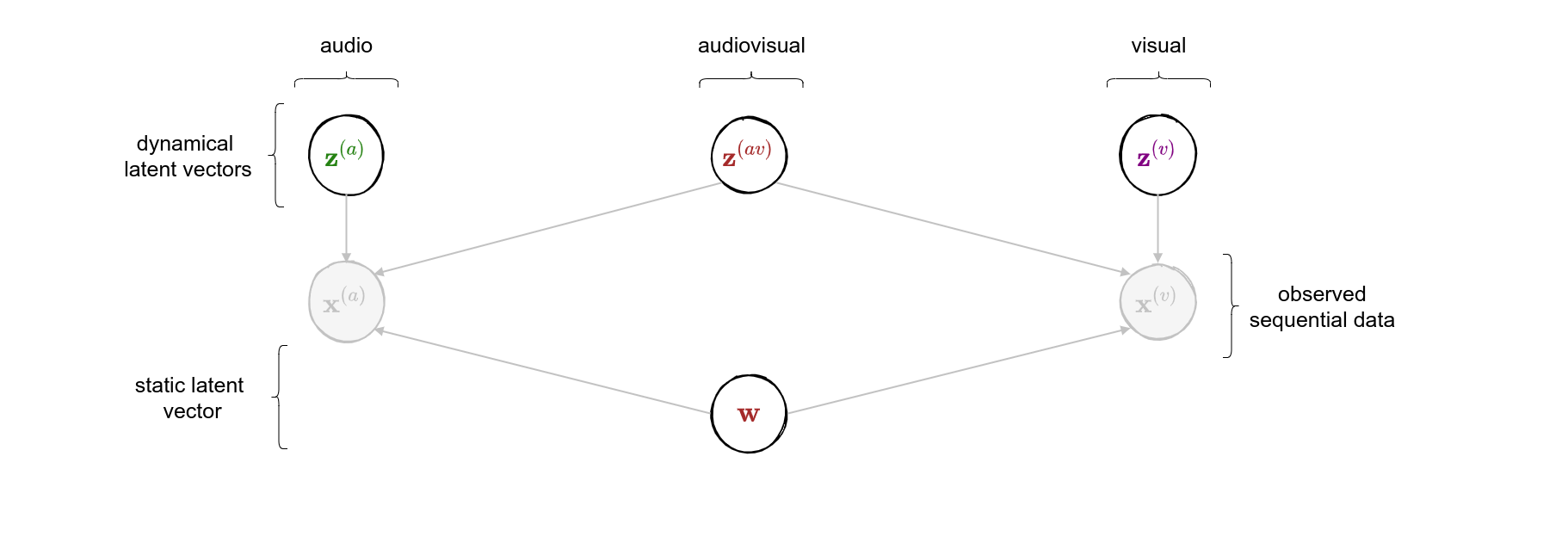] $$ \hspace{-.75cm} \small p\_\theta\left(\myxa{}, \myxv{}, \myzav{},\myza{},\myzv{}, \myw{}\right) = p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right)p\_\theta\left(\myxv{} \mid \myzav{}, \myzv{}, \myw{}\right) \boxed{p\_\theta\left(\myzav{}\right)p\_\theta\left(\myza{}\right) p\_\theta\left(\myzv{}\right)p\_\theta\left(\myw{}\right)} $$ --- class: middle count: false The global probabilistic graphical model of MDVAE is defined by the following Bayesian network. .center.width-100[] $$ \hspace{-.75cm} \small p\_\theta\left(\myxa{}, \myxv{}, \myzav{},\myza{},\myzv{}, \myw{}\right) = p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) p\_\theta\left(\myxv{} \mid \myzav{}, \myzv{}, \myw{}\right) p\_\theta\left(\myzav{}\right)p\_\theta\left(\myza{}\right) p\_\theta\left(\myzv{}\right)p\_\theta\left(\myw{}\right) $$ .alert[To complete the generative model, we also need to define the .bold[temporal dependencies] for the sequential variables.] --- class: middle .center.width-100[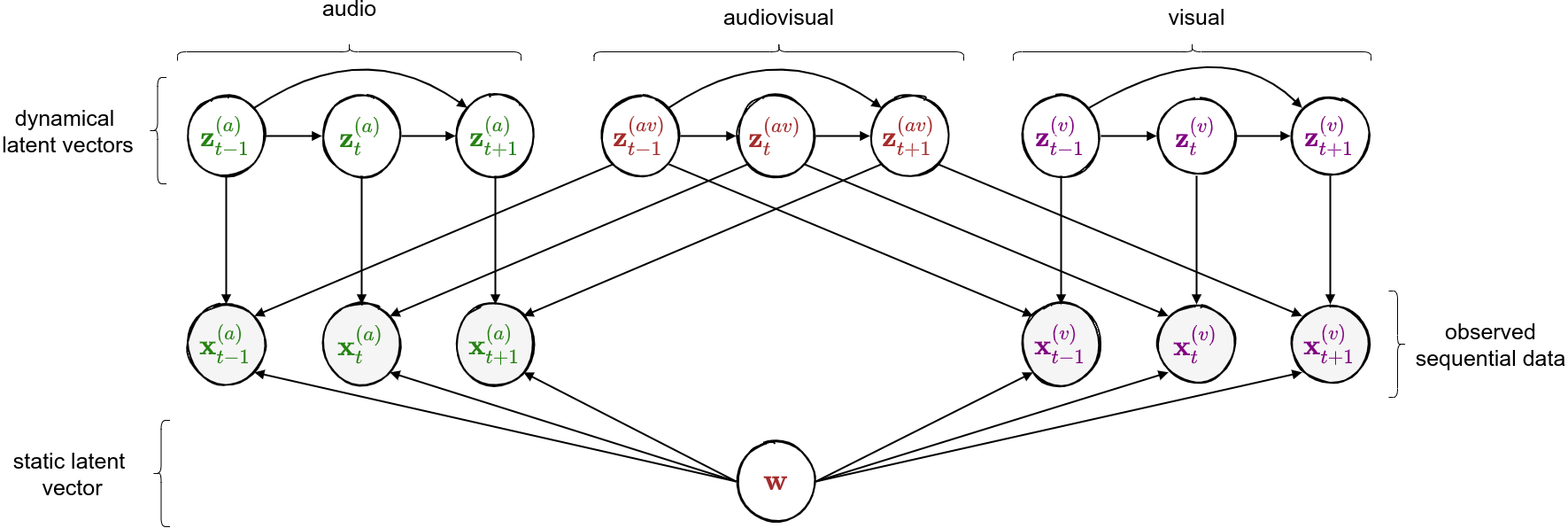] $$ \hspace{-.5cm} \small {p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxa{t} \mid \myzav{t},\myza{t},\myw{}\right)}, \hspace{.3cm} p\_\theta\left(\myxv{} \mid \myzav{},\myzv{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxv{t} \mid \myzav{t},\myzv{t},\myw{}\right) $$ $$ \hspace{-.5cm} \small p\_\theta\left(\myza{}\right) = \prod\_{t=1}^T p\_\theta\left(\myza{t} \mid \myza{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzav{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzav{t} \mid \myzav{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzv{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzv{t} \mid \myzv{1:t-1} \right) $$ --- class: middle count:false .center.width-100[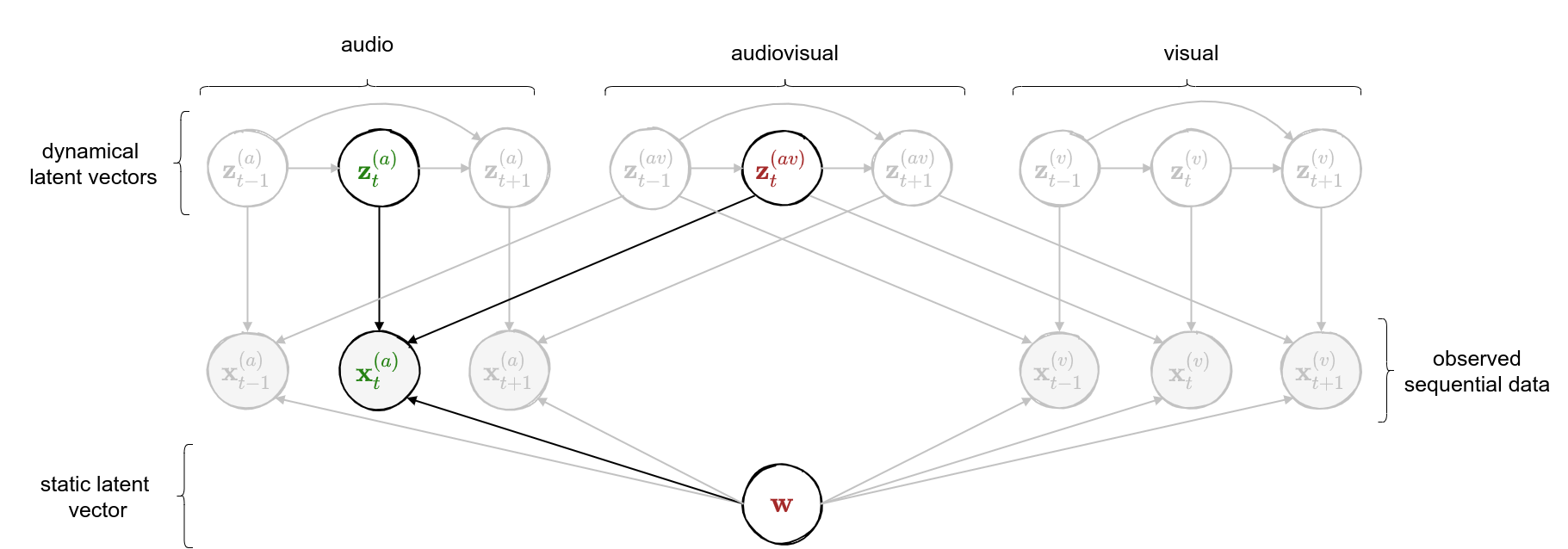] $$ \hspace{-.5cm} \small \boxed{p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxa{t} \mid \myzav{t},\myza{t},\myw{}\right)}, \hspace{.3cm} p\_\theta\left(\myxv{} \mid \myzav{},\myzv{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxv{t} \mid \myzav{t},\myzv{t},\myw{}\right) $$ $$ \hspace{-.5cm} \small p\_\theta\left(\myza{}\right) = \prod\_{t=1}^T p\_\theta\left(\myza{t} \mid \myza{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzav{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzav{t} \mid \myzav{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzv{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzv{t} \mid \myzv{1:t-1} \right) $$ --- class: middle count: false .center.width-100[] $$ \hspace{-.5cm} \small p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxa{t} \mid \myzav{t},\myza{t},\myw{}\right), \hspace{.3cm} \boxed{p\_\theta\left(\myxv{} \mid \myzav{},\myzv{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxv{t} \mid \myzav{t},\myzv{t},\myw{}\right)} $$ $$ \hspace{-.5cm} \small p\_\theta\left(\myza{}\right) = \prod\_{t=1}^T p\_\theta\left(\myza{t} \mid \myza{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzav{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzav{t} \mid \myzav{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzv{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzv{t} \mid \myzv{1:t-1} \right) $$ --- class: middle count: false .center.width-100[] $$ \hspace{-.5cm} \small p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxa{t} \mid \myzav{t},\myza{t},\myw{}\right), \hspace{.3cm} p\_\theta\left(\myxv{} \mid \myzav{},\myzv{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxv{t} \mid \myzav{t},\myzv{t},\myw{}\right) $$ $$ \hspace{-.5cm} \small \boxed{p\_\theta\left(\myza{}\right) = \prod\_{t=1}^T p\_\theta\left(\myza{t} \mid \myza{1:t-1} \right)}, \hspace{.3cm} \boxed{p\_\theta\left(\myzav{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzav{t} \mid \myzav{1:t-1} \right)}, \hspace{.3cm} \boxed{p\_\theta\left(\myzv{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzv{t} \mid \myzv{1:t-1} \right)} $$ --- class: middle count: false .small-nvspace[ ] .center.width-100[] $$ \hspace{-.5cm} \small {p\_\theta\left(\myxa{} \mid \myzav{},\myza{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxa{t} \mid \myzav{t},\myza{t},\myw{}\right)}, \hspace{.3cm} p\_\theta\left(\myxv{} \mid \myzav{},\myzv{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxv{t} \mid \myzav{t},\myzv{t},\myw{}\right) $$ $$ \hspace{-.5cm} \small p\_\theta\left(\myza{}\right) = \prod\_{t=1}^T p\_\theta\left(\myza{t} \mid \myza{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzav{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzav{t} \mid \myzav{1:t-1} \right), \hspace{.3cm} p\_\theta\left(\myzv{}\right) = \prod\_{t=1}^T p\_\theta\left(\myzv{t} \mid \myzv{1:t-1} \right) $$ These distributions are Gaussians parametrized by neural networks and $ \small p(\myw{}) = \mathcal{N}(\myw{}; \mathbf{0}, \mathbf{I})$. --- class: middle count: false .center[ # Multimodal dynamical VAE (MDVAE) ] <br> - Generative model - .bold[Inference model] - Two-stage training --- class: middle ## MDVAE inference model .vspace[ ] - As in the standard VAE, we need to define an inference model that approximates the posterior: $$ q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right) \approx p\_\theta\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right). $$ .vspace[ ] - The exact posterior is intractable, but using the chain rule, the Bayesian network of MDVAE and the D-separation principle .small[(Geiger et al., 1990; Bishop, 2006)], we can analyze the exact posterior dependencies, i.e. **how the observed and latent variables depend on each other given the observations**. See .small[(Girin et al., 2021)] for an extensive discussion of D-separation in the context of DVAEs. .vspace[ ] .credit[ L. Girin et al., Dynamical variational autoencoders: A comprehensive review, Foundations and Trends in Machine Learning, 2021. <br> D. Geiger et al., Identifying independence in Bayesian networks, Networks, 1990. <br> C. Bishop, Pattern Recognition and Machine Learning, Springer, 2006. ] --- .center.width-100[] The inference model $q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right)$ decomposes as the product of four terms: $$\hspace{-.5cm} q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right) \times q\_\phi\left(\myzav{}\mid \myxa{}, \myxv{}, \myw{} \right) \times q\_\phi\left(\myza{} \mid \myxa{}, \myzav{}, \myw{}\right) \times q\_\phi\left(\myzv{} \mid \myxv{}, \myzav{}, \myw{}\right)$$ --- count: false .center.width-100[] The inference model $q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right)$ decomposes as the product of four terms: $$\hspace{-.5cm} \boxed{ q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right)} \times q\_\phi\left(\myzav{}\mid \myxa{}, \myxv{}, \myw{} \right) \times q\_\phi\left(\myza{} \mid \myxa{}, \myzav{}, \myw{}\right) \times q\_\phi\left(\myzv{} \mid \myxv{}, \myzav{}, \myw{}\right)$$ --- count: false .center.width-100[] The inference model $q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right)$ decomposes as the product of four terms: $$\hspace{-.5cm} q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right) \times \boxed{ q\_\phi\left(\myzav{}\mid \myxa{}, \myxv{}, \myw{} \right) } \times q\_\phi\left(\myza{} \mid \myxa{}, \myzav{}, \myw{}\right) \times q\_\phi\left(\myzv{} \mid \myxv{}, \myzav{}, \myw{}\right)$$ --- count: false .center.width-100[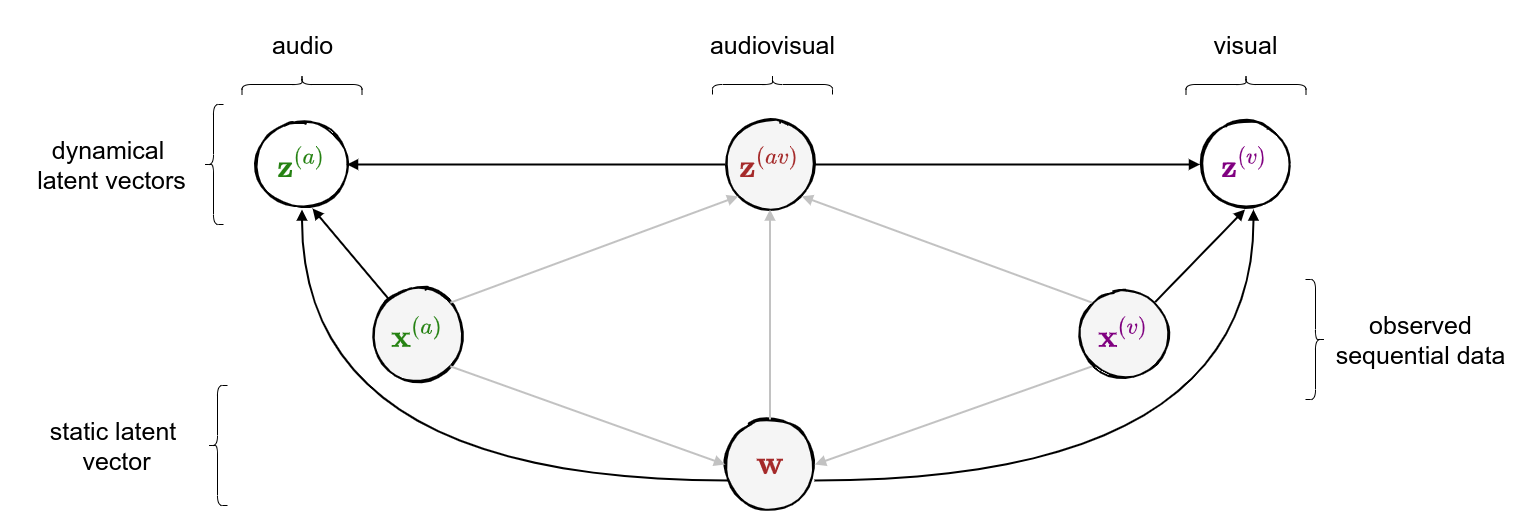] The inference model $q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right)$ decomposes as the product of four terms: $$\hspace{-.5cm} q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right) \times q\_\phi\left(\myzav{}\mid \myxa{}, \myxv{}, \myw{} \right) \times \boxed{ q\_\phi\left(\myza{} \mid \myxa{}, \myzav{}, \myw{}\right) } \times \boxed{ q\_\phi\left(\myzv{} \mid \myxv{}, \myzav{}, \myw{}\right) } $$ --- count: false .center.width-100[] The inference model $q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right)$ decomposes as the product of four terms: $$\hspace{-.5cm} q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right) \times q\_\phi\left(\myzav{}\mid \myxa{}, \myxv{}, \myw{} \right) \times q\_\phi\left(\myza{} \mid \myxa{}, \myzav{}, \myw{}\right) \times q\_\phi\left(\myzv{} \mid \myxv{}, \myzav{}, \myw{}\right)$$ .center[To complete the inference model, we also need to look at the **posterior temporal dependencies** for the dynamical latent variables $\myzav{}$, $\myza{}$ and $\myzv{}$.] --- class: middle Using again the chain rule, MDVAE Bayesian network and the D-separation principle, we have: $$ \begin{aligned} q\_\phi\left(\myzav{}\mid \myxa{}, \myxv{}, \myw{} \right) & = \prod\limits\_{t=1}^T q\_\phi\left(\myzav{t} \mid \myzav{1:t-1},\, \myxa{t:T},\, \myxv{t:T},\, \myw{} \right) \\\\ q\_\phi\left(\myza{} \mid \myxa{}, \myzav{}, \myw{}\right) & = \prod\limits\_{t=1}^T q\_\phi\left(\myza{t} \mid \myza{1:t-1},\, \myxa{t:T},\, \myzav{t},\, \myw{}\right) \\\\ q\_\phi\left(\myzv{} \mid \myxv{}, \myzav{}, \myw{}\right) & = \prod\limits\_{t=1}^T q\_\phi\left(\myzv{t} \mid \myzv{1:t-1},\, \myxv{t:T},\, \myzav{t},\, \myw{}\right) \end{aligned} $$ These distributions and $q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right)$ are Gaussians parametrized by neural networks. .footnote[Drawing the corresponding probabilistic graphical model at inference time would be difficult and not really informative.] --- class: middle count: false .center[ # Multimodal dynamical VAE (MDVAE) ] <br> - Generative model - Inference model - .bold[Two-stage training] --- class: middle ## ELBO As in the standard VAE, learning the MDVAE generative and inference model parameters consists in maximizing the **ELBO** $$\begin{aligned} \mathcal{L}(\phi, \theta) &= \underbrace{\mathbb{E}\_{q\_\phi\left(\myzav{},\, \myza{},\, \myzv{},\, \myw{} \mid \myxa{},\, \myxv{}\right)} \left[\ln p\_\theta\left(\myxa{}, \myxv{} \mid \myzav{},\myza{},\myzv{}, \myw{}\right)\right]}\_{\text{reconstruction accuracy}} \\\\ & \hspace{1cm} - \underbrace{D\_{\text{KL}}\left(q\_\phi\left(\myzav{},\myza{},\myzv{}, \myw{} \mid \myxa{}, \myxv{}\right) \Big\lvert\Big\rvert\, p\_\\theta\left(\myzav{},\myza{},\myzv{}, \myw{}\right) \right)}\_{\text{regularization}}. \end{aligned} $$ Developing this expression is a bit more complicated than with the standard VAE, but there is no fundamental difficulty. --- class: middle ## Two-stage training with the VQ-VAE - Standard VAEs tend to reconstruct **blurred outputs**, which is particularly true for image data. - The **vector-quantized VAE** (VQ-VAE) .small[(van den Oord et al., 2017)] learns a **discrete latent representation** to overcome this limitation. Before being fed to the decoder, the continuous latent vector is **quantized** using a **discrete codebook** that is jointly learned with the network architecture. .center.width-60[] - We exploit the VQ-VAE to **train the MDVAE in two stages**. .credit[A. van den Oord et al., Neural discrete representation learning, NeurIPS 2017.] --- class: middle .center[The first stage consists in learning a **VQ-VAE** independently for **each modality** and without **temporal modeling**.] .center.width-80[] .alert[Rather than learning the MDVAE on the raw audio and visual data, we will use the intermediate compressed representation of the VQ-VAEs before quantization.] --- class: middle .center[ In the second stage, **we learn the MDVAE model "inside" the frozen VQ-VAE**. This 2-stage training improves the reconstruction quality, but it also speeds up the training of the MDVAE model. ] .small-vspace[ ] .center.width-100[] .small-vspace[ ] .alert[The disentanglement between static versus dynamical and modality-specific versus audiovisual latent speech factors occurs during this second training stage.] --- class: middle count: false .center[ # Experiments on audiovisual speech ] <br> - .bold[Qualitative analysis of the learned representations] - Audiovisual facial image denoising - Audiovisual speech emotion recognition --- class: middle ## MEAD: Multi-view Emotional Audio-visual Dataset .tiny[(K. Wang et al., 2020)] .grid[ .kol-1-2[ We use about **30 hours of audiovisual emotional speech** from the MEAD dataset - 48 speakers .small[(different for training and testing)] - 8 different emotions - 3 levels of intensity - 7 views .small[(we keep only the frontal view)] Preprocessing: - Face images are cropped, resized (64x64 resolution) and aligned. ] .kol-1-2[ .center.width-100[] .center[.small[Image credits: (K. Wang et al., 2020)]] ] ] .small-nvspace[ ] - STFT parameters for computing power spectrograms are chosen such that the audio frame rate is equal to the visual frame rate (30 fps). .credit[ K. Wang et al., MEAD: A Large-scale Audio-visual Dataset for Emotional Talking-face Generation, ECCV, 2020 ] --- class: middle, center The first set of experiments consists in studying what characteristics of the audiovisual speech data are encoded in $\myw{}$, $\myzav{}$, $\myzv{}$, and $\myza{}$. .small-vspace[ ] .center.width-90[] .small-vspace[ ] <!-- We will present qualitative results obtained by swapping some of these latent variables from one audiovisual speech sequence to another. --> .alert[We will present qualitative results obtained by reconstructing an audiovisual speech sequence using some of the latent variables from another sequence.] --- class: middle, center .grid[ .kol-1-2[ We transfer $\myzav{}$ from the central sequence in red to the surrounding sequences. .center[ <video controls width="450" loop autoplay muted> <source src="demo/mosaic/z_av.mp4" type="video/mp4"> </video> ] Lip and jaw movements are transfered. ] .kol-1-2[ We transfer $\myzv{}$ from the central sequence in red to the surrounding sequences. .center[ <video controls width="450" loop autoplay muted> <source src="demo/mosaic/z_visual.mp4" type="video/mp4"> </video> ] Head and eyelid movements are transfered. ] ] --- class: middle, center .small-nvspace[ ] We transfer $\myzav{}$ and $\myzv{}$ from the central sequence in red to the surrounding sequences. The identity and global emotional state are preserved because $\myw{}$ is unaltered. .center[ <video controls width="650" loop autoplay muted> <source src="demo/swap_w_visual.mp4" type="video/mp4"> </video> ] --- class: middle .center[Interpolation of the static audiovisual latent variable $\myw{}$] .grid[ .kol-1-2[ .center[ <video controls width="400" loop autoplay muted> <source src="demo/interpolation/identity_interpolation.mp4" type="video/mp4"> </video> ] .caption[Same emotion, different identities.] ] .kol-1-2[ .center[ <video controls width="400" loop autoplay muted> <source src="demo/interpolation/emotions_interpolation.mp4" type="video/mp4"> </video> ].caption[Same identity, different emotions.] ] ] $$ \small \hspace{-.5cm} p\_\theta\left(\myxv{} \mid \myzav{},\myzv{},\myw{}\right) = \prod\_{t=1}^T p\_\theta\left(\myxv{t} \mid \myzav{t},\myzv{t},\boxed{\tilde{\myw{}}\_t}\right), \hspace{.3cm} \tilde{\myw{}}\_t = \alpha\_t \myw{} + (1- \alpha\_t) \myw{}', \hspace{.3cm} \alpha\_t = (T-t)/(T-1). $$ --- class: middle - The qualitative analysis confirmed that: - The static audiovisual latent variable $\myw{}$ encodes the speaker's identity and global emotional state. - The dynamical audiovisual latent variable $\myzav{}$ encodes the speaker's lip and jaw movements. - The dynamical visual latent variable $\myzv{}$ encodes the remaining facial movements such as the eyes and head movements. - These conclusions are confirmed quantitatively by measuring the impact of swapping latent variables on the action units (not presented today). --- class: middle count: false .center[ # Experiments on audiovisual speech ] <br> - Qualitative analysis of the learned representations - .bold[Audiovisual facial image denoising] - Audiovisual speech emotion recognition --- class: middle - We artificially **corrupt the visual modality** by adding random Gaussian noise on localized regions of the 6 central frames of a 10 frame-long sequence. The **audio modality is unaltered**. .center.width-70[] - The task is to denoise the visual modality. - We compare MDVAE with two **unimodal baselines** trained on the visual modality only: - .bold[VQ-VAE] .small[(van den Oord et al., 2017)], **no temporal modeling**. - .bold[DSAE] .small[(Li and Mandt, 2018)], same **temporal model** as MDVAE and trained in **two stages** as MDVAE. .alert[Denoising is done by simply encoding and decoding the corrupted (audio)visual speech sequence.] .credit[Y. Li and S. Mandt, "Disentangled sequential autoencoder", ICML 2018.] --- class: middle, black-slide .center.width-100[] --- class: middle, black-slide .center.width-100[] --- class: middle .grid[ .kol-3-5[ .center.width-95[] ] .kol-2-5[ <br> - Results are obtained by averaging over 200 test sequences. - Metrics are computed on the corrupted region. .small-vspace[ ] .alert-90[ The performance gap between MDVAE and the unimodal baselines is larger for the corruption of the mouth region. This is because MDVAE exploits the audio modality.] ] ] --- class: middle count: false .center[ # Experiments on audiovisual speech ] <br> - Qualitative analysis of the learned representations - Audiovisual facial image denoising - .bold[Audiovisual speech emotion recognition] --- class: middle - The qualitative analysis of the latent representations learned by MDVAE suggests that the static audiovisual latent variable $\myw{}$ encodes the speaker's emotion. - We propose to use the **mean vector of the Gaussian inference model** $q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right)$ as the input of a **multinomial logistic regression model** trained for emotion classification on the MEAD dataset (8 classes). - The mean vector is simply obtained by a forward through the encoder network corresponding to $q\_\phi\left(\myw{} \mid \myxa{}, \myxv{}\right)$. - We compare the performance of MDVAE with its **unimodal counterparts**: - .bold[A-DSAE] relies on the audio-only inference model $q\_\phi\left(\myw{} \mid \myxa{}\right)$; - .bold[V-DSAE] relies on the visual-only inference model $q\_\phi\left(\myw{} \mid \myxv{}\right)$. --- class: middle .center.width-80[] - Using the exact same experimental protocol, MDVAE outperforms its two unimodal counterparts by about 50% of accuracy. - With less than 10% of the labeled data, MDVAE reaches 90% of its maximal performance. --- .small-vspace[ ] .grid[ .kol-2-3[ - We also evaluate the audiovisual emotion classification performance on RAVDESS .small[(Livingstone and Russo, 2018)]. - We compare with a state-of-the-art model based on an audiovisual transformer architecture .small[(Chumachenko et al., 2022)]. .small-vspace[ ] <style type="text/css"> .tg {border-collapse:collapse;border-color:#ccc;border-spacing:0;} .tg td{background-color:#fff;border-color:#ccc;border-style:solid;border-width:0px;color:#333; font-family:Arial, sans-serif;font-size:18px;overflow:hidden;padding:10px 5px;word-break:normal;} .tg th{background-color:#f0f0f0;border-color:#ccc;border-style:solid;border-width:0px;color:#333; font-family:Arial, sans-serif;font-size:18px;font-weight:normal;overflow:hidden;padding:10px 5px;word-break:normal;} .tg .tg-2t70{border-color:#ffffff;font-size:18px;text-align:center;vertical-align:middle} .tg .tg-2t71{border-color:#ffffff;font-size:18px;text-align:center;vertical-align:middle} .tg .tg-y6or{border-color:#ffffff;font-size:18px;font-weight:bold;text-align:center;vertical-align:middle} </style> <table class="tg"> <thead> <tr> <th class="tg-2t70"></th> <th class="tg-2t70">F1 score (%)</th> <th class="tg-2t70">Precision (%)</th> <th class="tg-2t70">Recall (%)</th> </tr> </thead> <tbody> <tr> <td class="tg-2t70">Audiovisual transformer <br> <font size="-1">(Chumachenko et al., 2022)</font></td> <td class="tg-2t71">88.65</td> <td class="tg-2t71">89.37</td> <td class="tg-2t71">87.96</td> </tr> <tr> <td class="tg-2t70">MDVAE w/o finetuning <br>+ multinomial logisitic reg. </td> <td class="tg-2t71">82.86</td> <td class="tg-2t71">81.98</td> <td class="tg-2t71">83.76</td> </tr> <tr> <td class="tg-2t70">MDVAE w/ finetuning <br>+ multinomial logisitic reg. </td> <td class="tg-y6or">89.62</td> <td class="tg-y6or">89.55</td> <td class="tg-y6or">89.71</td> </tr> </tbody> </table> ] .kol-1-3[ .center.width-100[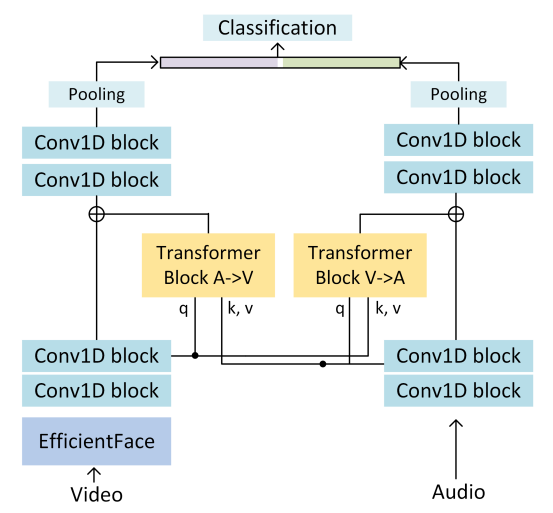] .center.small[Credits: (Chumachenko et al., 2022)] .small[**EfficientFace** is pre-trained on **AffectNet**, the largest dataset of in-the-wild facial images labeled in emotions.] ] ] .footnote[ Finetuning MDVAE is unsupervised. <br> ] .credit[ S.R Livingstone and F.A. Russo, "The Ryerson Audio-Visual Database of Emotional Speech and Song (RAVDESS): A dynamic, multimodal set of facial and vocal expressions in North American English", PloS one, 2018.<br> K. Chumachenko et al., "Self-attention fusion for audiovisual emotion recognition with incomplete data", arXiv preprint arXiv:2201.11095, 2022. ] --- class: middle exclude: true # Conclusion - We proposed the MDVAE to learn structured representations of multimodal and dynamical data. - Experimental results on audiovisual speech have shown that the model effectively combines the audio and visual information in static ($\myw{}$) and dynamical ($\myzav{}$) latent variables: - Talking faces can be synthesized by transfering $\myzav{}$ from one sequence to another, which preserves the speaker's identity, emotional state and visual-only facial movements. - The audio modality provides robstuness with respect to corruption of the visual modality on the mouth region. - The static audiovisual latent variable $\myw{}$ can be used for emotion recognition with few labeled data, and with much better accuracy compared with unimodal baselines. --- class: middle # Conclusion We proposed the MDVAE to learn structured representations of multimodal and dynamical data. - .bold[Why?] Collecting labels for every scenario and tasks is intractable, we need **alternatives to supervised learning**. - .bold[How?] **Deep generative** modeling is a powerful **unsupervised** learning paradigm that can be applied to many different types of data, in particular **multimodal** and **sequential data**. We can learn **structured** and **interpretable representations** by **modeling probabilistic dependencies** between observed and latent variables. - .bold[What?] **Various** applications in **audiovisual speech** processing, using **one single model**. --- class: middle MDVAE effectively combines the audio and visual information in static ($\myw{}$) and dynamical ($\myzav{}$) latent variables: - Talking faces can be synthesized by transfering $\myzav{}$ from one sequence to another, which preserves the speaker's identity, emotional state and visual-only facial movements. - The audio modality provides robstuness with respect to corruption of the visual modality on the mouth region. - The static audiovisual latent variable $\myw{}$ can be used for emotion recognition with few labeled data, and with much better accuracy compared with unimodal baselines. MDVAE is also competitive with a state-of-the-art method based on audiovisual transformers. --- class: middle Extensions and applications of MDVAE include: - audiovisual-consistent data augmentation using $p\_\theta\left(\myzv{}\right)$ and/or $p\left(\myw{}\right)$ for, e.g., automatic speech recognition; - deep speech prior for unsupervised audiovisual speech enhancement .small[(Sadeghi et al., 2020)]; - audiovisual voice conversion, provided we improve the audio speech generative model, e.g., inspiring from RAVE .small[(Caillon and Esling, 2021)]. .credit[M. Sadeghi et al., "Audio-visual speech enhancement using conditional variational auto-encoders", IEEE/ACM Transactions on Audio, Speech and Language Processing, 2020 <br> A. Caillon and P. Esling, "RAVE: A variational autoencoder for fast and high-quality neural audio synthesis", arXiv preprint arXiv:2111.05011, 2021] --- class: middle, center count: false # Thank you for your attention!