Signaux aléatoires

Brefs rappels de probabilité



Simon Leglaive


CentraleSupélec




Variable aléatoire

  • Une variable aléatoire \(X\) est une fonction qui associe à toute épreuve \(\omega\) dans l’univers \(\Omega\) une valeur dans un ensemble \(E\) :

    \[ X : \omega \in \Omega \mapsto X(\omega) \in E. \]

    Par exemple :

    • Pile ou face : \(\Omega = \{ \text{pile}, \text{face}\}, E = \{ 0, 1 \}\).
    • Taille d’un élève de CentraleSupélec : \(\Omega = ?, E = \mathbb{R}\) (il n’est souvent pas nécessaire d’expliciter \(\Omega\), en particulier pour une v.a. réelle).

  • Autrement dit, une variable aléatoire est une fonction qui attribue un nombre à chaque résultat possible d’une expérience aléatoire.

Espace de probabilité

Plus formellement, l’univers ou ensemble des épreuves \(\Omega\) (c’est l’ensemble des résultats possibles de l’expérience aléatoire) doit appartenir à un espace de probabilité (ou espace probabilisé) \((\Omega, \mathcal{F}, \mathbb{P})\), où :

  • \(\mathcal{F}\) est une tribu ou \(\sigma\)-algèbre sur \(\Omega\). C’est une collection de sous-ensembles « bien construits » de \(\Omega\) qu’on appelle événements.

    Par construction, une tribu satisfait certaines propriétés (non vide, contient \(\Omega\), stable par complémentaire, stable par union dénombrable, stable par intersection dénombrable).

    • Pour le jeu pile ou face : \(\mathcal{F} = \{\emptyset, \Omega, \text{pile}, \text{face}\}\).

    • Pour le prix du kilo de tomates, non seulement l’événement \(\{\omega : X(\omega) = c\}\) doit appartenir à \(\mathcal{F}\), mais aussi

      \[ \{\omega : a \le X(\omega) \le b\}, \qquad \{\omega : a \le X(\omega) \} \qquad \{\omega : X(\omega) \le b\} \]

      et beaucoup d’autres événements qui peuvent être intéressants selon telle ou telle situation.

      On souhaite que les opérations élémentaires \(\cup, \cap, ^c\) sur les événements de \(\mathcal{F}\) ne conduisent pas en dehors de cet ensemble, car nous aurons besoin d’évaluer la probabilité associée à ces opérations.

  • \(\mathbb{P}\) est une mesure de probabilité sur la tribu \(\mathcal{F}\) : à chaque événement \(A \in \mathcal{F}\) elle associe un nombre \(\mathbb{P}(A) \in [0, 1]\).

    Une mesure de probabilité satisfait les propriété suivantes :

    • Pour les événements \(A, B \in \mathcal{F}\), \(\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \cap B)\) et, si \(A\) et \(B\) sont disjoints, \(\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B)\).
    • \(\mathbb{P}(\emptyset) = 0\) et \(\mathbb{P}(\Omega) = 1\)

  • En résumé :

    On définit l’univers \(\Omega\) comme l’ensemble des résultats possibles d’une expérience aléatoire, puis on définit la tribu \(\mathcal{F}\) sur \(\Omega\) comme une collection de sous-ensembles « bien construits », et finalement on définit la mesure de probabilité \(\mathbb{P}\) sur la tribu \(\mathcal{F}\) qui permet d’associer un nombre \(\mathbb{P}(A) \in [0, 1]\) à tout événement \(A \in \mathcal{F}\).

    On obtient l’espace probabilisé \((\Omega, \mathcal{F}, \mathbb{P})\).

  • On a vu tout ce qui concerne l’ensemble de définition de la variable aléatoire, concentrons nous maintenant sur l’ensemble d’arrivée.

  • L’ensemble \(E\) doit être muni d’une tribu \(\mathcal{E}\) sur \(E\) afin de former un espace mesurable \((E, \mathcal{E})\).

    Par exemple, pour une variable aléatoire réelle, \(E = \mathbb{R}\) et on peut définir \(\mathcal{E} = \mathcal{B}(\mathbb{R})\) la tribu borélienne : la plus petite tribu sur \(\mathbb{R}\) contenant tous les ensembles ouverts.

  • La variable aléatoire \(X\) est alors en réalité une fonction mesurable sur \((E, \mathcal{E})\), c’est-à-dire que pour tout sous-ensemble \(B\) de la tribu \(\mathcal{E}\), l’image réciproque \(X^{-1}(B) = \{\omega : X(\omega) \in B\}\) appartient à la tribu \(\mathcal{F}\) et donc on peut calculer la probabilité \(\mathbb{P}(X^{-1}(B))\) grâce à la mesure de probabilité \(\mathbb{P}\) définie sur \((\Omega, \mathcal{F})\).

  • Cette définition permet de transposer l’aléa qui provient de \(\Omega\) dans l’espace \(E\).
  • On souhaite maintenant également transposer la mesure de probabilité \(\mathbb{P}\) sur \(E\).

Source: Wikipedia, \(\eta_X = \mathbb{P}_X\)

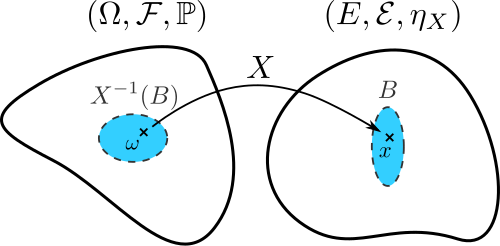
Loi de probabilité

  • On définit ainsi la probabilité que \(X\) prenne ses valeurs dans un sous-ensemble \(B\) de \(\mathcal{E}\) par :

    \[ \mathbb{P}_{X}(B) := \mathbb{P}(X^{-1}(B)) = \mathbb{P}(\{\omega : X(\omega) \in B\}),\]

    que l’on notera souvent plus simplement \(\mathbb{P}(X \in B)\).

  • \(\mathbb{P}_{X}\), appelée probabilité image de \(\mathbb{P}\) par \(X\), définit une mesure de probabilité sur \((E, \mathcal{E})\).

Source: Wikipedia, \(\eta_X = \mathbb{P}_X\)

L’ensemble des probabilités \(\mathbb{P}_{X}(B)\) pour tous les sous-ensembles \(B\) de la tribu \(\mathcal{E}\) définit la distribution ou loi de probabilité de \(X\).

Théorème de transfert et espérance

  • Pour toute fonction \(\varphi\) mesurable et intégrable au sens de Lebesgue définie sur \((E, \mathcal{E})\) :

    \[ \mathbb{E}\left[\varphi(X)\right] = \int_\Omega \varphi(X(\omega)) \, d \mathbb{P}(\omega) = \int_E \varphi(x) \, d \mathbb{P}_X(x). \]

  • Ce résultat permet de calculer l’espérance mathématique de \(X\) sans connaître l’espace de probabilité sous-jacent, en intégrant directement par rapport à \(\mathbb{P}_{X}\), la loi de \(X\) définie sur \((E, \mathcal{E})\).

Fonction de répartition

  • La loi de probabilité d’une v.a. est également entièrement caractérisée par sa fonction de répartition \[ F_X(x) = \mathbb{P}(X \le x) = \mathbb{P}(\{\omega : X(\omega) \le x\}) = \mathbb{P}_X(]-\infty, x]).\]

    Si deux variables aléatoires ont même fonction de répartition, alors elles ont même loi, et réciproquement.

  • La fonction de répartition permet de calculer la probabilité que \(X\) appartienne à un intervalle \(]a, b]\), \(a < b\) : \[ \mathbb{P}(a < X \le b) = \mathbb{P}(X \le b) - \mathbb{P}(X \le a) = F_X(b) - F_X(a). \]

  • On peut aussi calculer la probablité que \(X\) soit égale à un certain nombre \(x\):

    \[ \mathbb{P}(X = x) = \mathbb{P}(X \le x) - \mathbb{P}(X < x) = \mathbb{P}(X \le x) - \underset{h \rightarrow 0}{\lim} \mathbb{P}(X \le x - h) = F_X(x) - \underset{h \rightarrow 0}{\lim} F_X(x - h) \]

Variable continue et densité de probabilité

  • Pour une variable aléatoire continue, très souvent la fonction de répartition est différentiable par rapport à \(x\), ce qui revient à dire qu’il existe une densité de probabilité \(p_X(x)\) telle que :

    \[ F_X(x) = \int_{-\infty}^x p_X(y) dy, \]

    où \(p_X(x) \ge 0\) pour tout \(x \in \mathbb{R}\) et \(\displaystyle\int_{-\infty}^{+\infty} p_X(x) dx = 1\).

  • On a \(d\mathbb{P}_X(x) = p_X(x) dx\) et donc \[\mathbb{E}[X] = \int_\Omega X(\omega) \, d \mathbb{P}(\omega) = \int_E x \, d \mathbb{P}_X(x) = \int_{\mathbb{R}} x\,p_X(x) dx. \]

Variable discrète et masse de probabilité

  • Pour une variable aléatoire discrète, on définira souvent sa distribution via une fonction de masse de probabilité.

  • Si \(E = \{x_1, x_2, ... \}\) représente l’ensemble des valeurs possibles de la variable aléatoire \(X\), alors la fonction de masse de probabilité notée \(p_X(x)\) est définie par

    \[ p_X(x) = \begin{cases} \mathbb{P}(X = x) & \text{si } x \in E \\ 0 & \text{sinon} \end{cases}. \]

  • La loi de la variable est une somme pondérée de mesures de Dirac : \(\displaystyle \mathbb{P}_X = \sum_{i} \mathbb{P}(X = x_i) \delta_{x_i}\).

  • On a alors \[\mathbb{E}[X] = \int_\Omega X(\omega) \, d \mathbb{P}(\omega) = \int_E x \, d \mathbb{P}_X(x) = \int_E x \sum_{i} \mathbb{P}(X = x_i) d\delta_{x_i} = \sum_i x_i \,\mathbb{P}(X=x_i).\]

La fonction de répartition est :

  • continue pour une variable aléatoire continue :

    \[\underset{h \rightarrow 0}{\lim} F_X(x - h) = F_X(x)\]

    et donc \(\mathbb{P}(X = x) = 0\).

    Exemple: Loi normale / gaussienne.

  • en escalier pour une variable aléatoire discrète

    Exemple: Loi de Poisson.

Ressources

Pour plus d’informations sur les concepts de base de la théorie des probabilités, voir