import numpy as np
import soundfile as sf
import matplotlib.pyplot as plt
wavfile = './audio/CS.wav'
print(sf.info(wavfile))
x, fs = sf.read(wavfile)
t = np.arange(len(x)) / fs # Vecteur temps
plt.figure(figsize=(10, 3))
plt.plot(t, x, linewidth=0.5, color='black')
plt.title('Forme d\'onde d\'un signal de parole')
plt.xlabel('Temps (secondes)')
plt.ylabel('Amplitude')
plt.grid()Signaux aléatoires
Introduction
Signal audio analogique
- Une onde acoustique est émise lorsqu’une personne parle, lorsqu’un oiseau chante, lorsqu’un instrument de musique est joué, lorsque le vent souffle dans un feuillage, etc.
- L’onde acoustique se propage, par exemple dans l’air jusqu’à être captée par un microphone.
- Le microphone convertit l’onde acoustique en signal électrique.
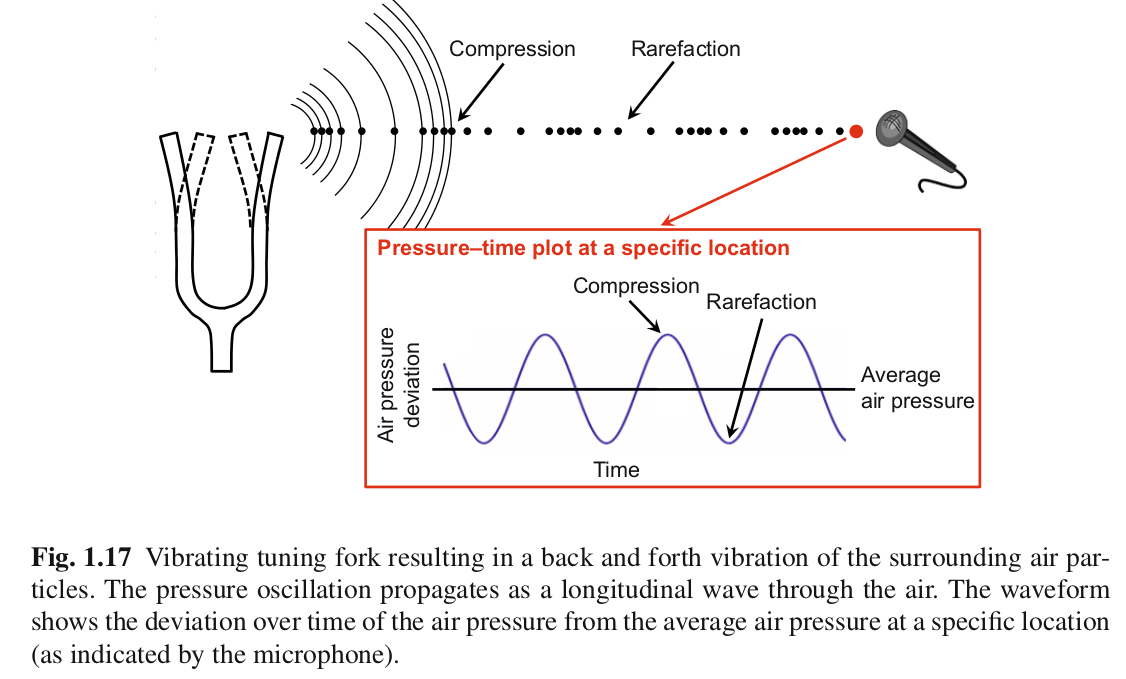
Image credit: Meinard Müller, “Fundamentals of Music Processing”, Springer 2015
Signal audio numérique
- Le signal analogique en sortie du microphone peut être converti en signal numérique via un convertisseur analogique-numérique (CAN).
- On obtient un signal échantillonné et quantifié.
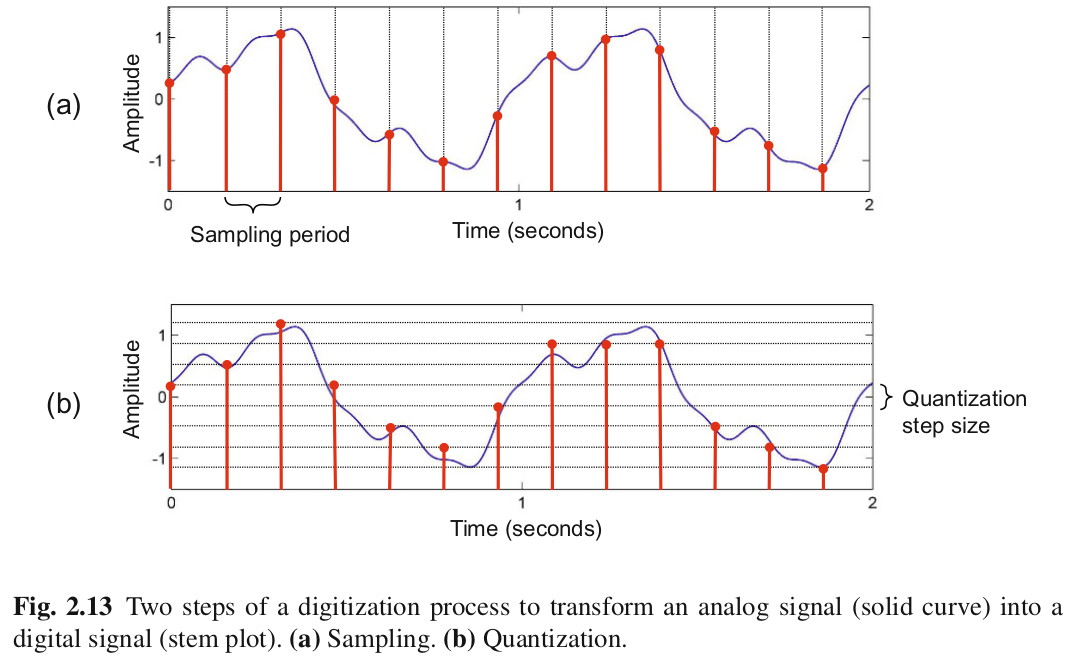
Image credit: Meinard Müller, “Fundamentals of Music Processing”, Springer 2015
Exemple d’un signal de parole
Voici un exemple de signal audio numérique extrait d’un fichier WAV.
./audio/CS.wav
samplerate: 16000 Hz
channels: 1
duration: 1.072 s
format: WAV (Microsoft) [WAV]
subtype: Signed 16 bit PCM [PCM_16]
Limites du traitement du signal déterministe
Revenons à notre signal de parole, pouvez-vous deviner à quel son chaque bloc correspond ?
- Le signal pour la consonne “s” ne peut pas être décrit par une fonction déterministe du temps.
- Une fonction déterministe suffisamment « flexible » pourrait approximer le signal sur un intervalle de temps donné, mais cette approximation ne serait pas valable en dehors de cet intervalle.
Le signal présente de nombreuses irrégularités, les valeurs observées semblent aléatoires.
Il est impossible de déterminer une règle permettant de caractériser le signal \(x(t)\) à tout instant \(t\) de manière unique et exacte.
- Considérons maintenant un signal de parole plus simple : l’enregistrement de la voyelle “A”.
- Il semble que l’on ait cette fois affaire à un signal quasi-périodique, que l’on pourrait peut-être modéliser par une fonction déterministe, au moins grossièrement.
- Mais cette modélisation serait-elle valable pour d’autres enregistrements de la voyelle “A” ?
Il y a certes des régularités, mais il y a aussi de nombreuses variations entre les enregistrements.
Cela pose la question de la modélisation d’un tel signal, et donc d’un tel phénomène physique.
🤔 Comment décrire mathématiquement le fait qu’un même phénomène physique engendre des signaux différents ?
La réponse réside dans une approche probabiliste.
L’observation d’un signal est considérée comme le résultat d’une expérience aléatoire.
On considère alors que l’échantillon \(x(t)\) à chaque instant \(t\) est une variable aléatoire.
L’évolution au cours du temps de cette variable aléatoire est ce qu’on appelle un signal aléatoire, ou plus généralement un processus aléatoire.
Chaque enregistrement de la voyelle “A” est une réalisation de ce processus aléatoire.
Cette approche probabiliste permet de prendre en compte la variabilité des signaux issus d’un même phénomène, par exemple physique, et de tenir compte des incertitudes liées à la mesure, aux erreurs de modélisation, etc.
Cela est très utile par exemple pour la reconnaissance de la parole, où l’on cherche à identifier les mots (ou autre unité de langage) prononcés par une personne, indépendamment du locuteur, du microphone, du bruit ambiant, etc.
