Signaux aléatoires

Modèles de signaux aléatoires

Simon Leglaive

CentraleSupélec

Au programme

Donner un peu de sens à tout ce qu’on a vu jusqu’ici, au travers de la présentation de quelques modèles de signaux aléatoires et de problèmes concrets en traitement du signal.
Nous reverrons certains de ces modèles de signaux en TD, où ce sera l’occasion de s’entraîner à calculer des moyennes, fonctions d’autocovariance, mesures spectrales de puissance, etc.

Bruit blanc

On appelle bruit blanc (faible) un processus \(\{X(t) \in \mathbb{R}\}_{t \in \mathbb{Z}}\) tel que :
- \(\mathbb{E}[X(t)] = 0\) et \(\mathbb{E}[X(t)^2] = \sigma^2 < + \infty\) pour tout \(t\) ;
- \(\mathbb{E}[X(t_1) X(t_2)] = 0\) si \(t_1 \neq t_2\).
On le notera \(\{X(t)\}_{t \in \mathbb{Z}} \sim BB(0, \sigma^2)\). Il s’agit d’un processus SSL.
Le bruit blanc est l’archétype du signal aléatoire.
Il sert de modèle aux processus stochastiques qui ne manifestent aucune structure temporelle et qui sont sans mémoire : les valeurs entre deux instants \(t_1\) et \(t_2\) tels que \(t_1 \neq t_2\) sont parfaitement décorrélées (mais pas nécessairement indépendante), aussi petite que soit la différence \(|t_1 - t_2|\).

Bruit blanc fort

On appelle bruit blanc fort un processus \(\{X(t) \in \mathbb{R}\}_{t \in \mathbb{Z}}\) tel que :
- \(\mathbb{E}[X(t)] = 0\) et \(\mathbb{E}[X(t)^2] = \sigma^2 < + \infty\) pour tout \(t\) ;
- les variables \(\{X(t) \in \mathbb{R}\}_{t \in \mathbb{Z}}\) sont indépendantes et identiquement distribuées (i.i.d).
On le notera \(\{X(t)\}_{t \in \mathbb{Z}} \sim IID(0, \sigma^2)\).
La structure de bruit blanc fort est plus contraignante que celle de simple bruit blanc, car les variables doivent être i.i.d et non seulement décorrélées.

Bruit blanc gaussien

Un bruit blanc gaussien est un bruit blanc pour lequel toutes les variables \(X(t)\) sont i.i.d suivant une loi gaussienne.
On le note \(\{X(t)\}_{t \in \mathbb{Z}} \sim BBG(0, \sigma^2)\) ou encore \(\{X(t)\}_{t \in \mathbb{Z}} \overset{i.i.d}{\sim} \mathcal{N}(0, \sigma^2)\).

Bruit de quantification

On considère le dispositif de quantification qui associe à un signal continu \(x(t) \in \mathbb{R}\) le signal quantifié \[ Y(t) = k q \quad \text{si} \quad x(t) \in \left[ kq - \frac{q}{2} , kq + \frac{q}{2} \right[,\]

où \(q\) s’appelle le pas de quantification et \(k \in \mathbb{Z}\).

On peut alors réécrire le signal quantifié comme \(Y(t) = x(t) + W(t)\) où \(W(t)\) représente l’erreur appelée bruit de quantification.
On modélise en général ce bruit comme un processus aléatoire sous les hypothèses suivantes : \(\{W(t)\}_t\) est une suite de variables aléatoires décorrélées qui suivent une loi uniforme sur l’intervalle \([-q/2, q/2]\).
En utilisant l’expression de la densité de probabilité de la loi uniforme on montre que \(\mathbb{E}[W(t)] = 0\) et \(\mathbb{E}[W(t)^2] = q^2 / 12\) donc \(\{W(t)\}_t\) est un bruit blanc.

Marche aléatoire continue

Une marche aléatoire continue est décrite par un processus \(\{X(t) \in \mathbb{R}\}_{t \in \mathbb{N}}\) tel que :

\[ X(t) = X(t-1) + W(t), \]

avec \(W(t) \overset{i.i.d}{\sim} \mathcal{N}(0, \sigma^2)\) et pour un certain « point de départ » \(X_0\).
La marche aléatoire modélise le cheminement d’un élève de CentraleSupélec qui essaie de rentrer chez lui / elle de puis la rue de la soif … mais aussi le prix d’une action en bourse, les gains et les pertes d’un joueur au casino, la dérive d’une horloge numérique, l’erreur de position d’un robot, etc.

Signal périodique à amplitude et phase aléatoires

Vous vous souvenez les voyelles du cours d’introduction ?
On a l’impression de voir un motif périodique se répéter, mais avec une amplitude et une phase à l’origine aléatoires.

Processus harmonique

Ce genre de phénomène peut se représenter à l’aide d’un processus harmonique : \[ X(t) = \sum_{k=1}^K A_k \cos(2 \pi \nu_k t + \phi_k), \]

où les amplitudes \(A_k \in \mathbb{R}\) et/ou les fréquences réduites \(\nu_k \in [-0.5, 0.5]\) et/ou les phases \(\phi_k \in [0, 2 \pi]\) peuvent être modélisées comme des variables aléatoires sous certaines hypothèses, notamment en matière de distribution de probabilité.

Par exemple, on peut supposer toutes les variables indépendantes et :

\(A_k \sim \mathcal{N}(0, \sigma_k^2)\) ;
\(\nu_k = k \, \nu_0\) avec \(\nu_0 \sim \mathcal{U}([a, b])\) et \(0 < a \le b < 0.5\) ;
\(\phi_k \sim \mathcal{U}([0, 2\pi])\).

Processus gaussien

Un processus gaussien est un processus aléatoire \(\{X(t)\}_{t}\) tel que pour tout ensemble fini d’instants \(t_1, t_2, \ldots, t_n\), le vecteur aléatoire \[ [X(t_1), X(t_2), \ldots, X(t_n)] \] suit une loi normale multivariée.
Il est entièrement caractérisé par :
- sa moyenne \(m_X(t) = \mathbb{E}[X(t)]\)
- sa fonction de covariance \(R_{XX}(t_1, t_2) = \mathbb{E}\left[(X(t_1) - m_X(t_1))(X(t_2) - m_X(t_2))\right]\)
Les processus gaussiens sont très utilisés car ils sont « faciles à manipuler » mathématiquement, et ils apparaissent naturellement dans de nombreux phénomènes physiques, notamment du fait du théorème central limite.

Processus gaussien pour la régression

Les processus gaussiens offrent un cadre probabiliste puissant pour les problèmes de régression, car ils permettent de modéliser non seulement la prédiction moyenne, mais aussi l’incertitude associée à chaque prédiction.

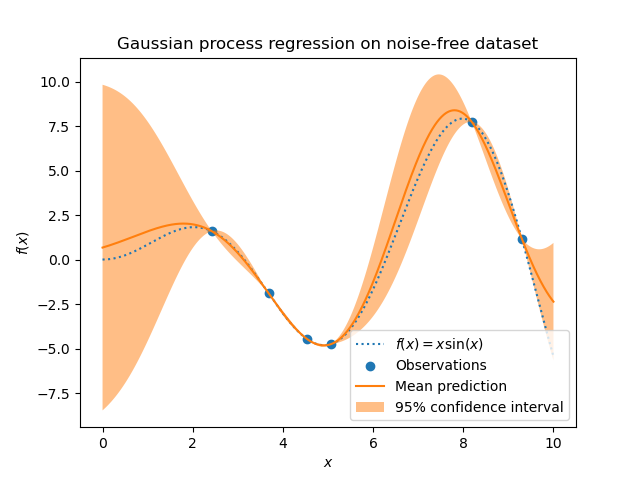
Processus gaussien pour la modélisation de la réverbération

En 1979, James Moorer, alors chercheur à l’IRCAM à Paris, remarqua que les réponses impulsionnelles des salles de concert « sonnent » comme un bruit blanc gaussien avec une enveloppe décroissant exponentiellement en temps. Il s’agit d’un processus gaussien non stationnaire.

On peut en effet invoquer le théorème central limite pour justifier qu’à partir d’une certaine densité d’échos qui se superposent, les coefficients de la réponse impulsionnelle de salle suivent une loi normale.

Cette technique, très simple et computationellement efficace, est toujours utilisée pour simuler la réverbération d’une salle, par exemple dans les contenus immersifs (RV, jeux vidéo, etc.) ou pour simuler des données d’entraînement de systèmes de traitement de la parole basés IA.

Annulation d’écho

Dans certaines situations, comme par exemple en téléphonie main-libre, un haut-parleur se trouve à proximité d’un microphone.

Le signal \(Y(t)\) en sortie du microphone contient donc le signal utile \(S(t)\) (la voix de la personne portant le téléphone) mais également un écho \(E(t)\) : \[ Y(t) = S(t) + E(t). \]

Crédit image : Alango Technologies

Cet écho est issu d’un haut-parleur duquel est émis un signal \(X(t)\) (la voix de la personne à distance) qui se propage dans un canal acoustique représenté par un filtre linéaire de réponse impulsionnelle \(h(t)\) :

\[ E(t) = [h \star X](t). \]
On modélise \(S(t)\) et \(X(t)\) comme des processus aléatoire réels, centrés, SSL.

Le problème d’annulation d’écho consiste donc à estimer le signal utile inconnu \(S(t)\) à partir des deux signaux observés \(Y(t)\) et \(X(t)\) avant de le transmettre à la personne distante.
On définit l’estimation du signal utile par :

\[ \hat{S}(t) = Y(t) - \hat{E}(t), \]

avec \(\hat{E}(t) = [g \star X](t)\) l’estimation de l’écho qu’on souhaite soustraire au signal capté par le microphone et \(g(t)\) la réponse impulsionnelle d’un filtre inconnu.
L’annulation d’écho revient donc à estimer le filtre \(g(t)\) qui minimise l’erreur quadratique moyenne : \[ \mathbb{E}\left[ (S(t) - \hat{S}(t) )^2 \right] = \mathbb{E}\Big[ \big(S(t) - Y(t) + [g \star X](t) \big)^2 \Big]. \]
Problème : cette expression n’est pas très utile, car elle fait intervenir \(S(t)\) qui n’est pas connu.

C’est là qu’entre en jeu une hypothèse supplémentaire.
En supposant que \(S(t)\) et \(X(t)\) sont décorrélés, on peut montrer que minimiser par rapport à \(\{g(t)\}_t\) l’expression précédente est équivalent à minimiser : \[ \mathbb{E}\left[ (Y(t) - [g \star X](t) )^2 \right], \]

expression qui cette fois ne fait intervenir que les signaux observés \(Y(t)\) (sortie du micro) et \(X(t)\) (sortie du haut-parleur).
Il s’agira ensuite de minimiser l’expression ci-dessus par rapport à \(\{g(t)\}_t\), mais ça c’est une autre histoire.

Hypothèses minimales du modèle pour l’annulation d’écho

\(S(t)\) et \(X(t)\) sont des processus aléatoires réels, centrés, stationnaires au second ordre.
\(S(t)\) est décorrélé de \(X(t)\).
L’écho \(E(t)\) est le résultat de la convolution d’un filtre \(h(t)\) avec \(X(t)\).