Gaussian mixture model estimation with the EM algorithm¶

Image credit: Bayesian Learning for Signal Processing, Antoine Deleforge, LVA/ICA 2015 Summer School.

Image credit: Bayesian Learning for Signal Processing, Antoine Deleforge, LVA/ICA 2015 Summer School.
import numpy as np
import scipy as sp
from scipy.stats import norm
from scipy.stats import multivariate_normal
import matplotlib
import matplotlib.pyplot as plt
from gmm_tools import plot_GMM, plot_data, generate_Bayes_adventures_data
np.random.seed(0)
On Tuesday October 7, 1949, Thomas Bayes is going to visit Oxford University. Upon arriving at the university, three prankster students throw dozens of small stones at him from the roof. Bayes wants to know which student has thrown which stone. Determined, he begins to note the 2D position of each single stone on the ground.
N = 500 # number of samples (number of stones)
D = 2 # number of dimensions (x and y coordinates)
gen = generate_Bayes_adventures_data(N, D)
x = gen[-1]
plot_data(x)
print(x.shape)
(500, 2)
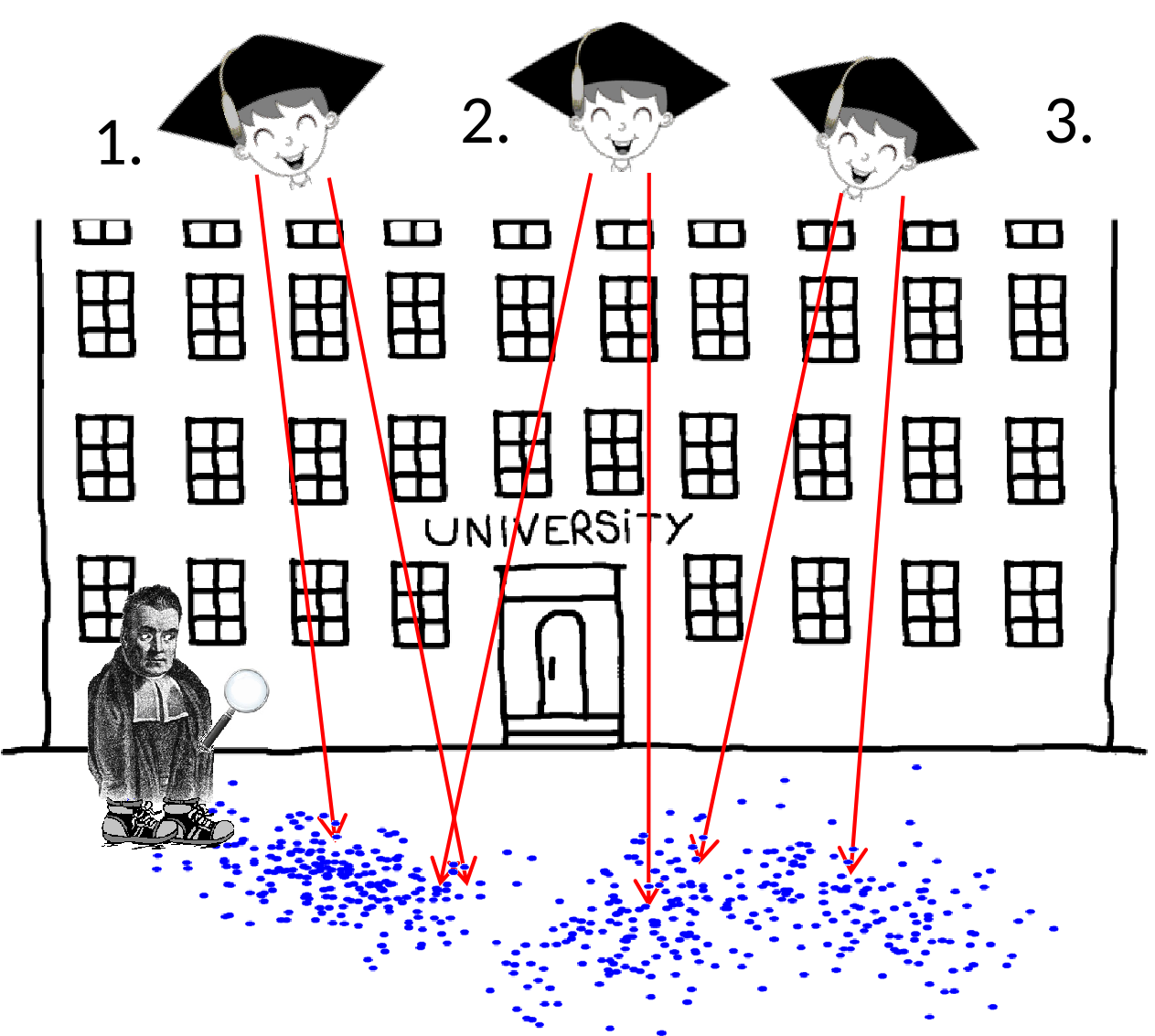
For his investigation, Thomas Bayes defines the generative process of the observed data as follows:
He observes a realization of a set of observed random variables denoted by $ \mathbf{x} = \{\mathbf{x}_n \in \mathbb{R}^2\}_{n=1}^N$, where $\mathbf{x}_n$ corresponds to the 2D position of the $n$-th stone.
These observations are generated from a set of latent unobserved random variables denoted by $ \mathbf{z} = \{z_n \in \{1,...,K\} \}_{n=1}^N$, where $z_n$ denotes the identity of the student (among $K=3$ students) who threw the $n$-th stone.
The relationships between the latent and observed variables are defined by their joint distribution, also called complete-data likelihood:
$$ \begin{aligned} p(\mathbf{x}, \mathbf{z}; \theta) &= \prod_{n=1}^N p(\mathbf{x}_n | {z}_n; \theta) p({z}_n; \theta) \\ &= \prod_{n=1}^N \prod_{k=1}^K \left( p(\mathbf{x}_n | {z}_n=k; \theta) p({z}_n=k; \theta) \right)^{\mathbb{1}\{z_n = k\}}, \end{aligned} $$where $\mathbb{1}\{z_n = k\} = \begin{cases}1 & \text{if } z_n = k \\ 0 & \text{otherwise}\end{cases}$.
The prior over the latent variables follows a categorical distribution: $$ p({z}_n=k; \theta) = \pi_k, \qquad k \in \{1,...,K\}, \qquad \text{with }\, \pi_k > 0\, \text{ and }\, \sum_{k=1}^K = 1. $$
The likelihood is Gaussian:
$$ p(\mathbf{x}_n | z_n=k; \theta) = \mathcal{N}(\mathbf{x}_n; \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k),$$with $\mathcal{N}(\mathbf{x}; \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \displaystyle \frac{1}{\sqrt{\det(2\pi \boldsymbol\Sigma)}} \exp\left(-\frac 1 2 ({\mathbf x}-{\boldsymbol\mu})^\mathrm{T}{\boldsymbol\Sigma}^{-1}({\mathbf x}-{\boldsymbol\mu})\right).$
The set of unknown deterministic model parameters is defined by:
$$ \theta = \{\pi_k, \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k\}_{k=1}^K. $$The complete-data log-likelihood is therefore given by: $$ \ln p(\mathbf{x}, \mathbf{z}; \theta) = \sum_{n=1}^N \sum_{k=1}^K \mathbb{1}\{z_n = k\} \left(\ln \pi_k + \ln \mathcal{N}(\mathbf{x}_n; \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k) \right). $$
How can you interpret the responsabilities?
In order to compute the responsabilities, it is necessary to estimate the unknown model parameters $\theta$. To do so, we would like to maximize the log-marginal likelihood $\ln p(\mathbf{x}; \theta) $. Give its expression and explain why it cannot be directly optimized.
Let $\tilde{\theta}$ denote the current estimate of the model parameters. Using the above definition of the complete-data log-likelihood, solve the E-step, that is compute the so-called $Q$-function, defined by:
$$\begin{aligned} Q(\theta, \tilde{\theta}) &= \mathbb{E}_{p(\mathbf{z} | \mathbf{x}; \tilde{\theta})}[\ln p(\mathbf{x}, \mathbf{z}; \theta)] \end{aligned}$$Make the depency on the model parameters $\theta = \{\pi_k, \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k\}_{k=1}^K$ explicit (any constant with respect to these parameters can be omitted).
Hints:
You now have to solve the M-step, that is updating the model parameters by maximizing $Q(\theta, \tilde{\theta})$ with respect to (w.r.t) $\theta$. To do so, you will simply cancel the partial derivatives of $Q(\theta, \tilde{\theta})$ w.r.t $\boldsymbol{\mu}_k$, $\boldsymbol{\Sigma}_k$ and $\pi_k$.
Useful matrix derivation formulas can be found in the appendix at the end of this notebook, or in the Matrix Cookbook.
Compute the partial derivative of $Q(\theta, \tilde{\theta})$ w.r.t $\boldsymbol{\mu}_k$ and set it to zero to get the update of $\boldsymbol{\mu}_k$.
$$\begin{aligned} \nabla_{\boldsymbol{\mu}_k} Q(\theta, \tilde{\theta}) &= \\ \end{aligned}$$You will express the update as a function of $N_k = \sum_{n=1}^N \tilde{r}_{n,k}$. If we interpret $\tilde{r}_{n,k}$ as being equal to 1 if $\mathbf{x}_n$ belongs to component $k$ and 0 otherwise, $N_k$ corresponds to the number of points assigned to cluster $k$.
Hint: $\boldsymbol{\Sigma}_k$ is a covariance matrix so it is symetric.
Compute the partial derivative of $Q(\theta, \tilde{\theta})$ w.r.t $\boldsymbol{\Sigma}_k$ and set it to zero to get the update of $\boldsymbol{\Sigma}_k$.
$$\begin{aligned} \nabla_{\boldsymbol{\Sigma}_k} Q(\theta, \tilde{\theta}) &= \\ \end{aligned}$$You will express the update as a function of $N_k = \sum_{n=1}^N \tilde{r}_{n,k}$.
Hint: Use the trace trick: $\mathbf{x}^\top\boldsymbol{\Sigma}^{-1}\mathbf{x} = tr(\mathbf{x}^\top\boldsymbol{\Sigma}^{-1}\mathbf{x}) = tr(\boldsymbol{\Sigma}^{-1}\mathbf{x}\mathbf{x}^\top) $ and then refer to the matrix derivation formulas in the appendix.
The update for $\pi_k$ is obtained by maximizing $Q(\theta, \tilde{\theta})$ under the constraint that $\sum_{k=1}^K \pi_k = 1$. We obtain:
$$ \pi_k = N_k / N, $$where $N_k = \sum_{n=1}^N \tilde{r}_{n,k}$. The optimal prior probablity $p(z_n = k) = \pi_k$ is thus given by the number of points $N_k$ in cluster $k$ divided by the total number of points $N$.
To obtain this expression you have to use the method of Lagrange multipliers:
you first cancel the partial derivative of the following Lagrangian w.r.t $\pi_k$:
$$ \mathcal{L}(\theta, \tilde{\theta}, \lambda) = Q(\theta, \tilde{\theta}) + \lambda \left(\sum_{k=1}^K \pi_k - 1\right). $$
then you simply inject this solution into the constraint to find out the solution for $\lambda$.
class GMM():
"""
Gaussian mixture model
"""
def __init__(self, n_comp, data_dim=2, seed=None):
super(GMM, self).__init__()
self.n_comp = n_comp
self.data_dim = 2
self.init_param(seed=seed)
def init_param(self, pis=None, means=None, covars=None, seed=None):
"""
Initialize the model parameters using the provided arguments
or randomly.
Inputs
pis: list of prior probabilities, length equal to self.n_comp
means: list of GMM means, length equal to self.n_comp
covars: list of GMM means, length equal to self.n_comp
Outputs
None
"""
if seed is not None:
np.random.seed(seed)
if pis is not None:
self.pis = pis
else:
self.pis = []
for k in np.arange(self.n_comp):
# prior set to 1/K
self.pis.append(1/self.n_comp)
if means is not None:
self.means = means
else:
self.means = []
for k in np.arange(self.n_comp):
# mean vector drawn from a centered unit Gaussian
mean = np.random.randn(self.data_dim)
self.means.append(mean)
if covars is not None:
self.covars = covars
else:
self.covars = []
for k in np.arange(self.n_comp):
# identity covariance
covar = np.eye(self.data_dim)
self.covars.append(covar)
if seed is not None:
np.random.seed()
def fit(self, data, n_iter=50):
"""
Fit a GMM with the EM algorithm
Inputs
data (number of points, dimension) array
n_iter
Outputs
log-marginal likelihood
"""
LML = []
for iter in np.arange(n_iter):
resp = self.E_step(data)
self.M_step(data, resp)
LML.append(self.compute_LML(data))
return LML
def E_step(self, data):
"""
Compute the responsabilities
Inputs
data (number of points, dimension) array
Outputs
responsabilities (number of points, number of GMM components)
"""
N = data.shape[0]
resp = np.zeros((N,self.n_comp))
###### TO COMPLETE ######
# Use the static method GMM.compute_pdf_multi_gaussian() defined below
#########################
return resp
def M_step(self, data, resp):
"""
Update the model parameters
Inputs
data: (number of points, dimension) array
Outputs
None
"""
###### TO COMPLETE ######
pass
#########################
def compute_LML(self, data):
"""
Compute the log-marginal likelihood
Inputs
data: (number of points, dimension) array
Outputs
log-marginal likelihood
"""
LML = 0
###### TO COMPLETE ######
# Use the static method GMM.compute_pdf_multi_gaussian() defined below
#########################
return LML
@staticmethod
def compute_pdf_multi_gaussian(data, mean, covar):
"""
Compute the pdf of a multivariate Gaussian distribution
Inputs
data: data points to evaluate the pdf (number of points, dimension) array
mean: mean vector (dimension,) array
covar: covariance matrix (dimension, dimension) array
Outputs
pdf evaluated on 'data', (number of points,) array
"""
rv = multivariate_normal(mean, covar)
return rv.pdf(data)
The GMM class defined in the previous cell implements a Gaussian mixture model. It has two important methods:
init_param() initializes the model parametersfit() runs the EM algorithm to estimate the model parameters. It alternates between the E- and M-steps, and after each iteration it computes the log-marginal likelihood.In the following cell, we instantiate this class for our problem.
gmm = GMM(n_comp=3, data_dim=2, seed=2)
Complete the method that computes the log-marginal likelihood (LML) and run the following cell.
The LML is defined as a sum over the data points. You will divide this sum by the number of data points, so that the value of the objective function does not depend on the size of the dataset. In other words, compute the mean instead of the sum.
LML_init = gmm.compute_LML(x)
print("log-marginal likelihood: %.4f" % LML_init)
if int(LML_init*1000) == -22548:
print("so far, it seems to be ok")
else:
print("argh, this is not the expected result, either you made a mistake, or my unit test is badly designed")
Complete the method that computes the E-step and run the following cell.
resp = gmm.E_step(x)
if np.sum(resp) == N:
print("so far, it seems to be ok")
else:
print("argh, this is not the expected result, either you made a mistake, or my unit test is badly designed")
To assign each point to each cluster, we simply look at the argmax of the reponsabilities. Run the following cell.
z_hat = np.argmax(resp, axis=1)
fig1 = plt.figure(figsize=(10,4))
ax1 = fig1.add_subplot(111)
plot_GMM(x, z_hat, gmm.means, gmm.covars, colors=['b','g','r'], ax=ax1)
ax1.set_title('estimation')
Can you explain what you observe?
Complete the method that computes the M-step and run the following cell.
Hint: Updating the covariance matrix requires computing the outer product of vectors. Look at the notebook numpy new axis trick to help you.
gmm.M_step(x, resp)
LML = gmm.compute_LML(x)
delta_LML = LML - LML_init
print("log-marginal likelihood: %.4f" % LML)
print("log-marginal likelihood improvement: %.4f" % delta_LML)
if int(delta_LML*1000) == 19556:
print("\nthe log-marginal likelihood increased, well done!")
else:
print("argh, this is not the expected result, either you made a mistake, or my unit test is badly designed")
LML = gmm.fit(data=x, n_iter=50)
In the following cell, we plot the log-marginal likelihood along the iterations. It should be monotonically increasing, a nice feature of the EM algorithm which is very useful for debugging: if the log-marginal likelihood decreases, there is a bug.
plt.plot(LML)
plt.title("log-marginal likelihood")
plt.xlabel("EM iterations")
Let's have a look to the results.
resp = gmm.E_step(x)
z_hat = np.argmax(resp, axis=1)
fig1 = plt.figure(figsize=(10,4))
ax1 = fig1.add_subplot(111)
plot_GMM(x, z_hat, gmm.means, gmm.covars, colors=['b','g','r'], ax=ax1)
ax1.set_title('estimation')
We used synthetic data, so we actually also know the true model parameters.
(pis_true, means_true, covars_true, z_true, _) = gen
fig2 = plt.figure(figsize=(10,4))
ax2 = fig2.add_subplot(111)
plot_GMM(x, z_true, means_true, covars_true, colors=['b','g','r'], ax=ax2)
ax2.set_title('ground truth')
This is not perfect, but not that bad either...
Question 3.4.1 - Re-run the complete pipeline several times after changing the random seed that is used to instantiate the GMM. Explain what you observe and propose a method to choose the best model among the ones you obtained from several runs.
Question 3.4.2 - Briefly explain the commonalities and differences between the K-means algorithm and the EM algorithm for the GMM model. You can use different sources of information, e.g.
It is your responsability to assess the reliability of the information you can find on the Internet.
Question 3.4.3 - Ask ChatGPT to complete the code below to perform image segmentation with the EM algorithm for the GMM model, using 3 clusters. You may need to install scikit-learn, if you don't want, ask ChatGPT to not use this package, but the code will be much longer and more difficult to read. Explain in one sentence how this image segmentation method works and explain what you observe in the result.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.mixture import GaussianMixture
# Load the grayscale image using matplotlib (it supports only PNG by default)
image = plt.imread('beatles_BW.jpg') # Replace with your grayscale image path
# Display the image
plt.imshow(image, cmap='gray') # Choose a colormap appropriate for visualization
plt.axis('off')
plt.show()
For $f: \mathbb{R}^{I \times J} \mapsto \mathbb{R}$, the gradient is defined by $\frac{d}{d \mathbf{X}} f(\mathbf{X}) = \nabla_{\mathbf{X}}f(\mathbf{X}) = [\frac{\partial}{\partial X_{ij}} f(\mathbf{X}) ]_{ij} $.
Below are some useful derivatives:
\begin{equation} \frac{\partial \mathbf{x}^T \mathbf{a}}{\partial \mathbf{x}} = \frac{\partial \mathbf{a}^T \mathbf{x}}{\partial \mathbf{x}} = \mathbf{a} \end{equation}\begin{equation} \frac{\partial \mathbf{x}^T \mathbf{A} \mathbf{x}}{\partial \mathbf{x}} = 2 \mathbf{A} \mathbf{x}, \qquad \text{if } \mathbf{A} \text{ is symmetric} \end{equation}\begin{equation} \frac{\partial}{\partial \mathbf{X}}tr(\mathbf{A}\mathbf{X}^T) = \mathbf{A} \label{derTrace1} \end{equation}\begin{equation} \frac{\partial}{\partial \mathbf{X}}tr(\mathbf{A}\mathbf{X}) = \mathbf{A}^T \label{derTrace2} \end{equation}\begin{equation} \frac{\partial}{\partial \mathbf{X}}tr(\mathbf{X}^{-1}\mathbf{A}) = -(\mathbf{X}^{-1}\mathbf{A}\mathbf{X}^{-1})^T \label{derTraceInverse} \end{equation}\begin{equation} \frac{\partial}{\partial \mathbf{X}}\ln \det(\mathbf{X}) = \big((\mathbf{X}^T)^{-1}\big)^T \end{equation}